Outline
Mercator
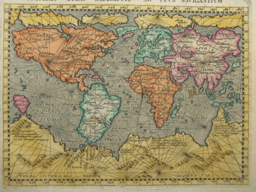
Toen Ralph de Meester, student aan de Hogere Zeevaartschool, me contacteerde met GeoGebravragen over de mercatorprojectie ontmoetten twee werelden elkaar. Ralph leerde me alles over orthodromen en loxodromen en ik leerde hem de GeoGebra geheimen van rijen en krommen. Samen slaagden we erin om interactief in één applet een route tegelijk op een aardbol en een wereldkaart te tonen. Hopelijk helpt dit boek ook anderen om te ontdekken dat Mercator geen onhandige tekenaar was die een vreselijk vervormde kaart tekende, maar een geniaal cartograaf die de zeevaart die handige kaart bezorgde waar ze om vroegen.
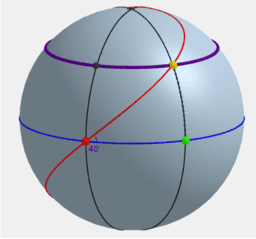
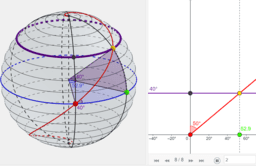
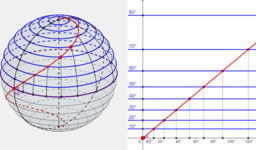
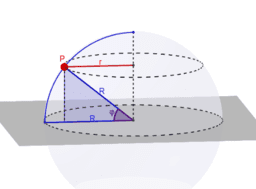
Hoe kunnen we de aardbol voorstellen op een plat vlak? Hoe kunnen we kaarten maken die bruikbaar zijn in de navigatie? Wat is de kortste route tussen twee punten op de aardbol? In dit boek verken je de oplossing die Gerard Mercator in de 16e eeuw bedacht om een wereldkaart te tekenen die revolutionair was voor de scheepvaart en wiskundig zijn tijd ver vooruit was. Meteen leer je ook waarom dat de continenten zo vervormd zijn en waarom vaar- en vliegroutes gebogen lijnen zijn op een wereldkaart.
De applets in dit boek zijn gebaseerd op het werk van Rafael Losada Liste https://www.geogebra.org/m/uT3czZnE die het fantastische idee en het nodige geduld had om op een bol de continenten te tekenen met een veelhoekslijn.
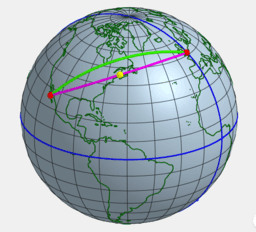
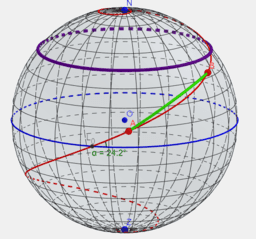
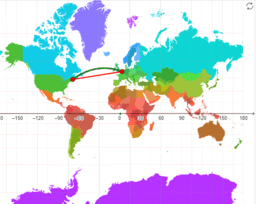
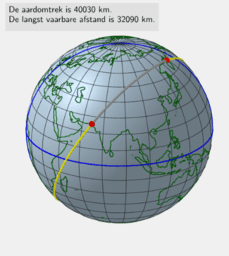
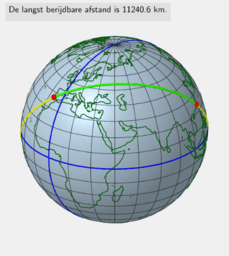
Als extraatje krijg je de langste rechte lijn die je kunt bezeilen op aarde en de langste route die je kunt berijden. Op kaart lijken het helemaal geen rechte lijnen, maar op de aardbol zie je duidelijk dat de trajecten wel degelijk recht zijn.
Op https://www.geogebra.org/m/dsbbxbwe vind je een algemeen boek over kaartprojecties en diverse opties om kaarten te tekenen.
When Ralph de Meester, student at the Antwerp Maritime Academy, contacted me with GeoGebra questions on the mercator projection two worlds met each other. Ralph explained me all about orthodromes and loxodromes and I explained him the GeoGebra secrets of Sequences and curves. Together we succeeded in representing routes on a globe and on a world map in one interactive applet. Hopefully this book can help others too to discover that Mercator wasn't a lousy drawer who made a terribly deformed map, but a genious cartographer who offered navigators the useful map they were asking for.
How can we represent a globe on a map? How can we make useful maps for navigation? What's the shortest route between two points on the globe? In this book you can explore the 16th century solution of Gerard Mercator that was revolutionary for navigation and mathematically its time far ahead. At the same time you'll learn why the continents look so deformed and why boats and planes follow curved trajectories on a world map.
The applets of this book are based on the work of Rafael Losada Liste https://www.geogebra.org/m/uT3czZnE who had the fantastic idea and the patience needed to depict the continents on a sphere using a polyline.
As an extra you get the longest sailable Line Path on Earth and th longest drivable Line Path on Earth. On the World map they don't look like straight Lines, but the path on the globe confirms they're on Great Circles.
On https://www.geogebra.org/m/dsbbxbwe you can find a more general book on map projections