Dikdörtgenler Prizması Açınımları M.5.2.5.2
GİRİŞ

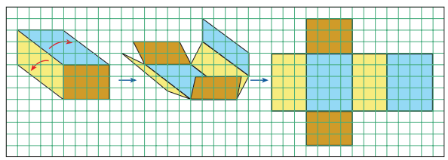
Bu küpün üretimi için nasıl bir planlama yapılmış olabilir? Kâğıda küpün tüm yüzlerini görebilecek bir çizim yapmak sizce mümkün müdür? Nasıl?
Yukarıdaki materyalde görmüş olduğunuz dikdörtgenler prizmasının açılımında hangi çokgenler bulunur? Neden?
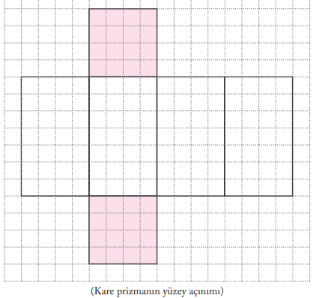
Ayrıt uzunluklarını en:2 boy:2 yükseklik:4 şeklinde yaptığımız dikdörtgenler prizmasının açılımında hangi çokgenler mevcut olur? Neden? Önceki derste işlediğimiz bilgilere göre bu dikdörtgenler prizmasının özel adı nedir?
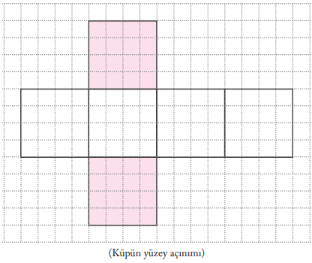
Bütün ayrıt uzunlukları eşit olan dikdörtgenler prizmasının açılımında hangi çokgenler mevcut olur? Önceki derste işlediğimiz bilgilere göre bu dikdörtgenler prizmasının özel adı nedir?
Verilen cevaplara göre dikdörtgenler prizması, kare prizma ve küp arasında nasıl bir bağıntı oluşmaktadır? Açıklayınız.