Combinare disequazioni goniometriche elementari
COMBINARE LE DISEQUAZIONI: UNIFORMARE INTERVALLO E PERIODICITÀ
Per le disequazioni più complesse, in cui si devono poter confrontare i risultati di due disequazioni parziali (tipicamente perché le si sta confrontando in uno studio del segno) è opportuno riportare tutte le soluzioni nello stesso intervallo di angoli - di solito si sceglie quello tra 0° e 360°.
Supponiamo ad esempio di dover risolvere la disequazione:
Si tratta di una disequazione fratta, di cui conosciamo la logica risolutiva.
1) Innanzitutto dobbiamo porre le condizioni di esistenza
Le seconde C.E. sono quelle per l'esistenza della tangente, ovvero che . Non risolviamo qui le C.E. perché non sono la cosa che ci interessa affrontare in questo momento.
2) dobbiamo poi studiare il segno di numeratore e denominatore
Vedi che la prima disequazione è l'esempio dell'ultima animazione proposta, mentre sviluppando i calcoli della seconda si ottiene il penultimo esempio proposto. Ricopiamo quindi qui i risultati ottenuti.
3) A questo punto dovremmo costruire un grafico e combinare i segni.
Si vede però dopo poco che non è impresa facile: la prima soluzione inizia con un valore negativo e si ferma a 90° (ma sappiamo che vi sono altri valori sul cerchio), mentre la seconda considera solo valori positivi (quindi non sappiamo come si comporta per angoli negativi) e per contro il suo segno varia sull'intero cerchio.
Per poter mettere le soluzioni su un unico grafico e combinarne i segni è necessario riportarle nello stesso intervallo, e con la stessa periodicità. In questo caso adattiamo la soluzione di A riportandola nell'intervallo [0°-360°]. Per farlo ci aiutiamo riproducendo il cerchio goniometrico che contiene le soluzioni di A.
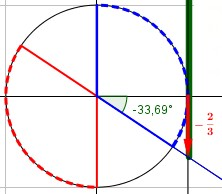
La soluzione riportata nell'intervallo 0°-360° diventa quindi
Abbiamo trascurato la periodicità perché ci stiamo concentrando nell'intervallo 0°-360°. Ora possiamo riportare in un unico grafico il segno di A e quello di B, per ottenere il segno risultante della frazione, come mostrato nell'animazione qui sotto.
Ci accorgiamo che la soluzione rossa si è adattata non solo in termini dell'intervallo in cui era definita (originariamente la soluzione era presa tra -90° e +90°, e l'abbiamo spostata da 0° in avanti) ma anche in termini di periodicità (360° e non più 180°): dato che il comportamento di B ha bisogno di 360° per essere definito (è solo dopo un intero giro che vediamo l'intero alternarsi di segni e e che questo schema inizia a ripetersi uguale a se stesso), dovremo riportare anche i segni di A per 360°, anche se sappiamo che da un certo punto in poi è la ripetizione dello stesso schema: solo in questo modo potremo vedere tutte le diverse combinazioni di segni di A e di B.
In generale avremo che se la periodicità dei due contributi è diversa, dovremo considerare un intervallo pari al minimo comune multiplo delle due periodicità, cioè al primo intervallo che contiene un numero intero di cicli per entrambi i contributi. La periodicità della soluzione sarà pari a questo periodo comune.
Puoi trovare due esercizi svolti che chiariscono questo concetto al seguente indirizzo:
https://drive.google.com/open?id=0Bxf-VRarLuQqclVwVzRVeWxJalU