PROBABILIDAD DE EVENTOS MUTUAMENTE EXCLUYENTES
OBJETIVO
Que el alumno conozca los conceptos básicos de la Teoría de Probabilidades, que pueda distinguir en diversas situaciones de azar eventos que son independientes o mutuamente excluyentes y que reflexione sobre la Ley Débil de los grandes números.
EXPLORA
En una ruleta como la siguiente, se hace girar la fecha para obtener un resultado al azar.
Analiza los siguientes casos y responde. Explica tus respuestas.
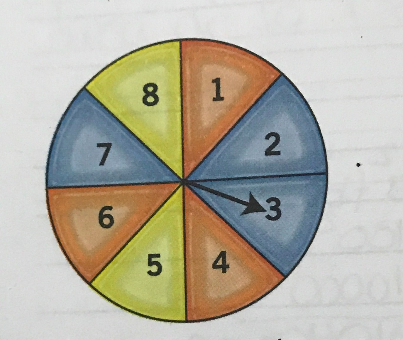
a) ¿Cuál es la probabilidad de que la fecha se detenga en un sector con un número mayor que 5?
_______________________________________________________________________________________
b) ¿Cuál es la probabilidad de que se detenga en un sector amarillo y con un número mayor que 5?
_______________________________________________________________________________________
c) ¿Cuál es la probabilidad de que la fecha se detenga un sector amarillo o con un múltiplo de 3?
_______________________________________________________________________________________
d) Calcula la probabilidad de que se obtenga un sector amarillo o con un múltiplo de 3.
_______________________________________________________________________________________
e) Calcula la probabilidad de que la flecha se detenga en un sector amarillo que tenga un múltiplo de 3.
_______________________________________________________________________________________
CONOCE
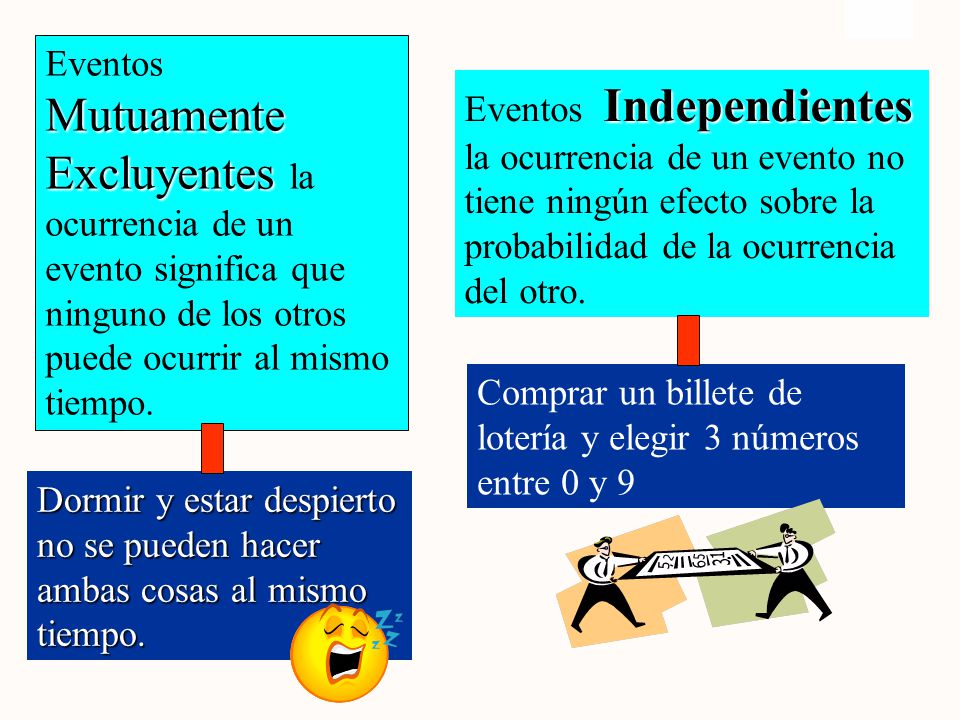
EVENTOS.. PROBABILIDAD ESO 3(2)
OBSERVA Y APRENDE
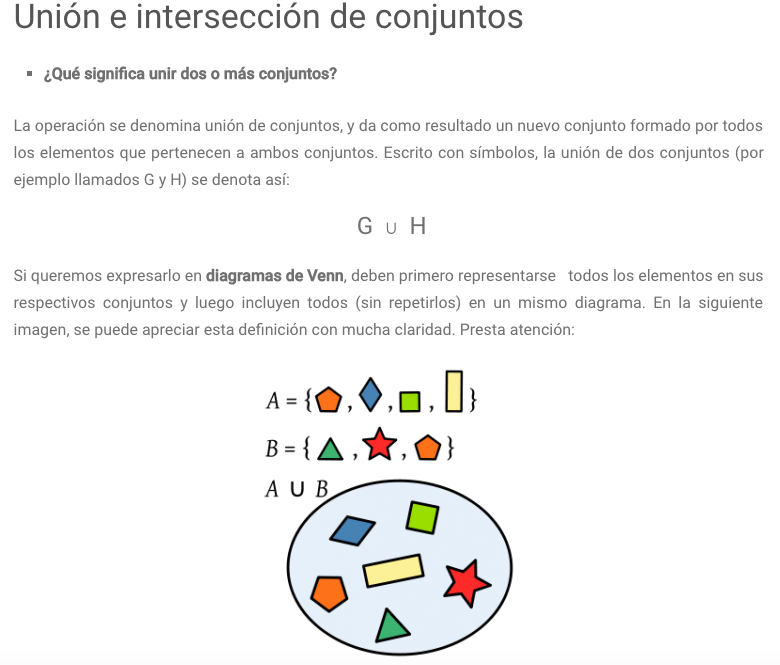


NOTA:
Si dos eventos son mutuamente excluyentes, la probabilidad de que ocurra cualquiera de los dos es igual a la suma de sus probabilidades. Así, si A y B son mutuamente excluyentes, entonces . A esto se le conoce como regla de la suma.
EJEMPLO:
Se tienen cinco libros de distintas materias: Matemática, Biología, Química, Física y Lenguaje. Si se toma uno de ellos, ¿cuál es la probabilidad de que este sea de matemática o de física?
Solución:
Sean los eventos
A ≡Tomar el libro de Matemáticas.
B ≡Tomar el libro de Física.
La probabilidad pedida es:
P(A∪B) = P(A) + P(B) -P(A∩B)
Como A y B son eventos mutuamente excluyentes, P(A∩B) = 0.
Por lo tanto, la probabilidad pedida nos queda:
P(A∩B) = (1/5)+(1/5)-0= 2/5
PRACTICA
EN UN EXPERIMENTO ALEATORIO SE LANZA UN DADO REGULAR Y SE OBSERVA EL NÚMERO QUE CAE. ESCRIBE LOS ELEMENTOS DE LOS EVENTOS A,B,C Y D QUE SE DESCRIBEN A CONTINUACIÓN.
A) Cae un número que es múltiplo de 3. __________________
B) Cae un número par: _________________________________
C) Cae un número primo: _______________________________
D) Cae un número menor que 5: _________________________
DESCRIBE LOS SIGUIENTES EVENTOS Y ANOTA SUS ELEMENTOS.
________________________________________________
: ___________________________________________________
: _______________________________________________
_______________________________________________
_______________________________________________
