Plaza, juegos y matemática…?

Construcción de una función por tramos, utilizando Geogebra, en su modalidad Fotogebra. 

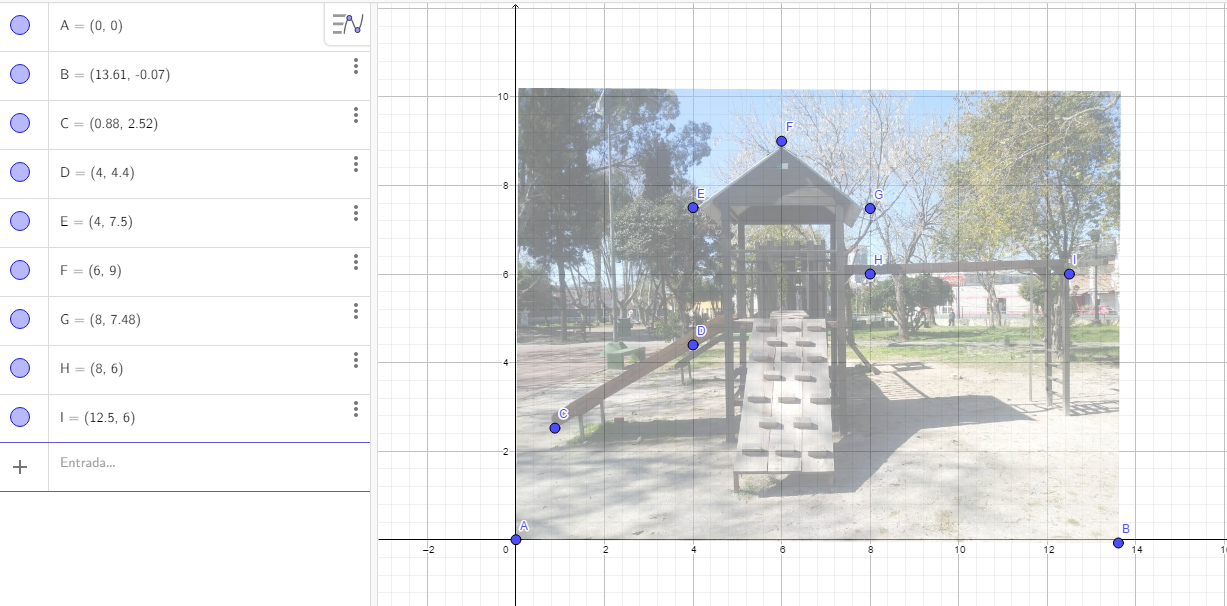
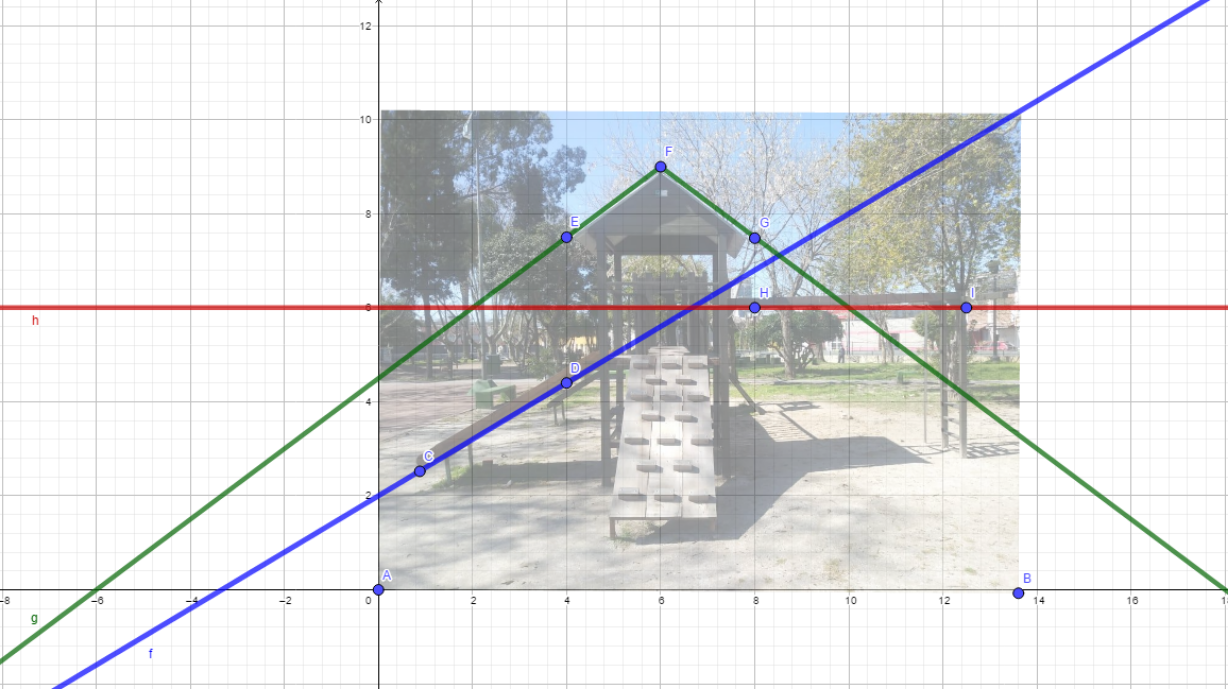
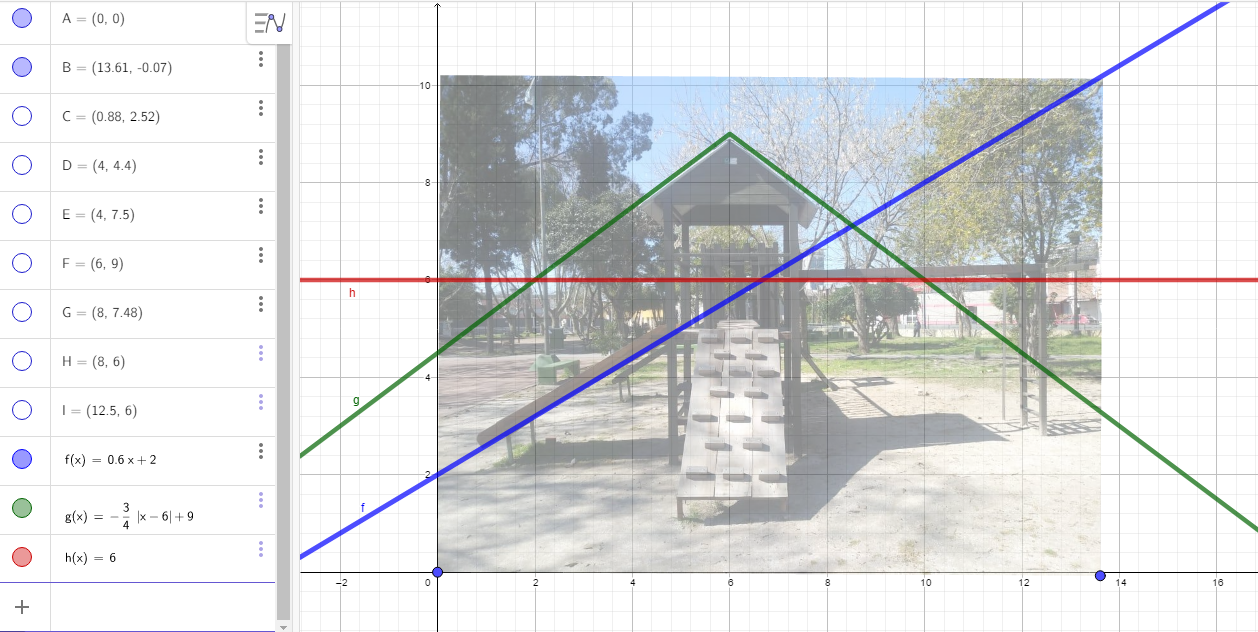
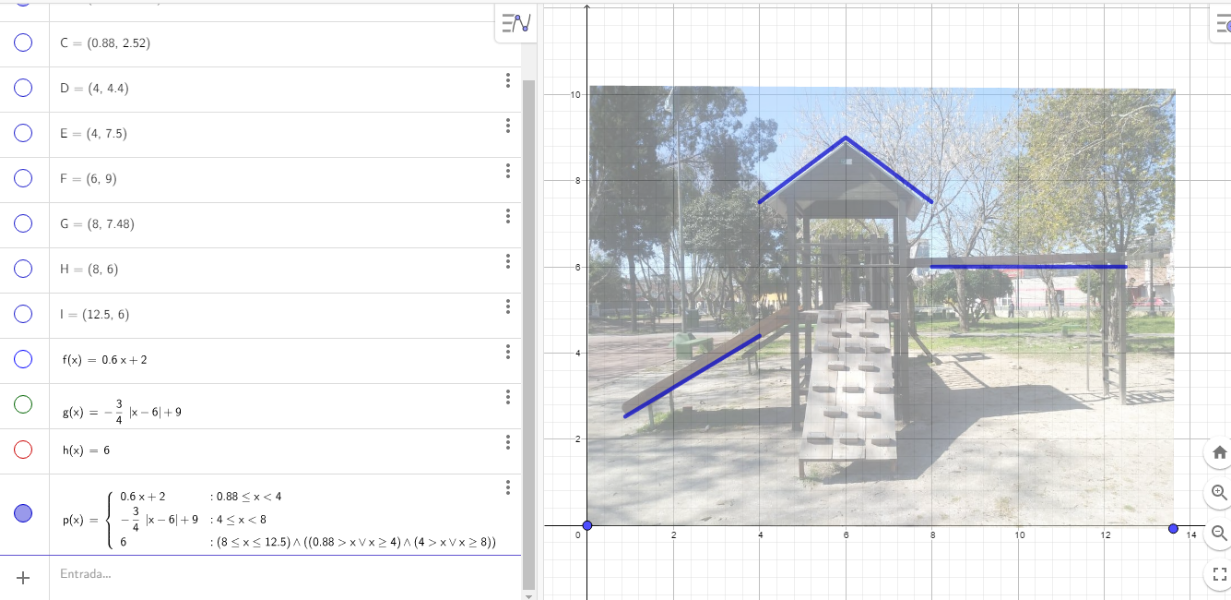
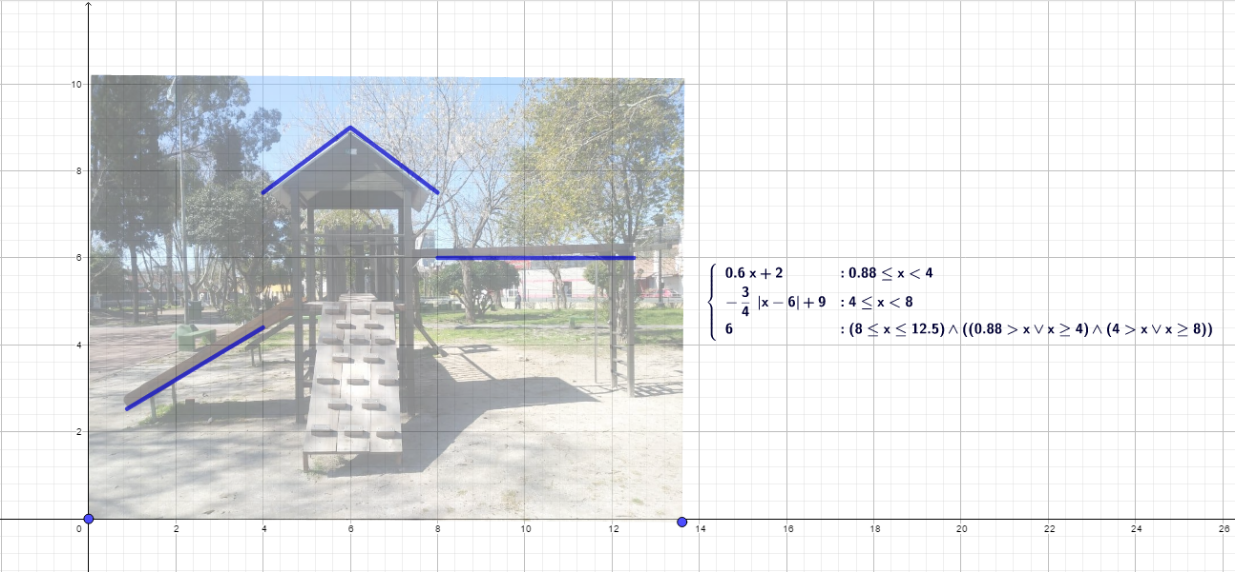
Actividad propuesta: Para debatir entre todos: David, Javier y Marcelo son amigos desde la época en la que cursaban el Profesorado de Matemática. Se conocieron y enseguida descubrieron que compartían un hobby: la fotografía. Para plasmar su afición en un álbum grupal decidieron captar con sus cámaras una imagen que los devuelva a la infancia. Para ello recorrieron la Plaza Félix Bernal y lograron congelar con las lentes un juego de toboganes, puentes y escaladas. Inmediatamente después de revisar la imagen reconocieron que es posible conjugar el arte de la fotografía con sus conocimientos matemáticos: Intentaron describir partes del juego construyendo una función definida por tramos.

Utilizando la fotografía tomada por los amigos, intentar dar respuesta a los siguientes interrogantes:

¿Es posible que este grupo de amigos logre su cometido? ¿Qué tipo de funciones podrían haber utilizado para construir la función partida? Describirlas.
Indicar el dominio y la imagen de la función por tramos que construyeron.

¿Podrán ustedes encontrar otra imagen que se pueda describir utilizando funciones?

Resolución Geométrica-algebraica

Aproximación al objetivo… Función lineal: Sabiendo que

y que la forma general de la función lineal es: f:

/ f(x) = y = mx + b Sea C

(0,88; 2,52) y D

(4; 4,4) dos puntos que pertenecen a la recta, luego reemplazando se tiene que: m =

m =

m = 0,6 Luego, sustituyendo el valor de "m" y uno de los puntos que pertenecen a la recta, D

(4; 4,4), en la formula general se tiene que: y = 0,6 x + b 4,4 = 0,6 . 4 + b 4,4 - 2,4 = b

b = 2 Luego, volviendo a la forma general y reemplazando el valor de "b" concluimos que: f (x) = 0,6 x + 2 Función valor absoluto: Forma general de la función valor absoluto de x con vértice V

(h; k): f:

/g(x) =a |x-h| + k Sea P

(0; 4,5) el punto de Intersección de la grafica f(x) con el eje "oy" y sea V

(6; 9) el vértice de la función. Sustituyendo ambos puntos en la formula general se tiene que: g(x) =a |x-h| + k 4,5 = a |0-6| + 9 ,despejando resulta: 4,5 - 9 = a |-6| -4,5 = a . 6

a=-0,75=

Luego, volviendo a la forma general y reemplazando el valor de "a" y de V concluimos que: g(x) = |x - 6| + 9 Función constante: Sabiendo que la forma general de la función constante es: h(x) = k ; k

Por lo tanto, la función constante es: h(x) = 6

Presentación de las funciones de manera individual:

Modelo terminado Presentación de la función definida por tramos:

Plaza, juegos y matemática…?

Nuevos recursos

Descubrir recursos

Descubre temas