Öklid bağıntıları
İç açılardan birinin 90 derece olan üçgene dik açılı üçgen denir.
İki üçgenin karşılıklı ikişer açıları eş ise bu üçgenler benzerdir. Benzerlik oranı olarak ise; eşit açıların karşısındaki kenarların uzunlukları oranı yazılır.
Diklik kavram, dik üçgen ve benzerliği hatırladığımıza göre öklid teoremine geçelim
Bir dik üçgende dik açının olduğu köşeden karşı kenara indirilen dikme için bazı eşitlikler tanımlanır. Şimdi bunları bulmaya çalışacağız
EAC üçgeniyle ECB üçgenlerinin benzer üçgenler olduğunu benzerlik konusundan biliyoruz.
Bu iki üçgen bezer olduğu için AC/EA =AB/CB dir buradan nasıl bir bağıntı elde edebilirsiniz ?
Benzer şekilde AE/EC = EC/EB eşitliğini kullanarak nasıl bir bağıntı elde edebilirsiniz ?
bulduğunuz bağıntıda h(yükseklik) ile p yada k arasında bir ilişki var mıdır ? Yüksekliğimiz artarsa p ve k için ne söylenebilir ?
Sürgüden CBA açısının değerini değiştirin ve ne gözlemlediğinizi yazınız.
applet üzerinde ACB üçgeninin h,p,k,a ve b kenarlarının uzunluklarını hesaplayınız. sürgümüzdeki değer yardımıyla kenar uzunluklarımızı değiştirdikçe bulduğunuz bağıntının hala geçerli mi olup olmadığını inceleyiniz.
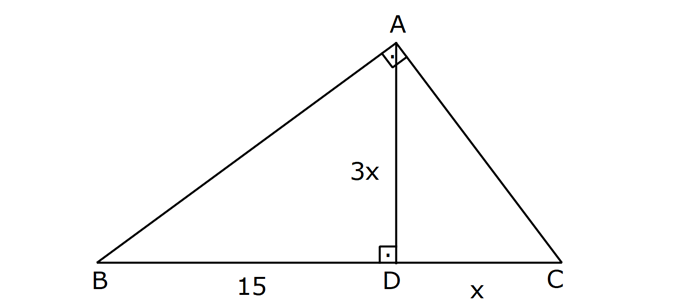
yukarıdaki dik üçgende verilen x uzunluğunu nedir ?
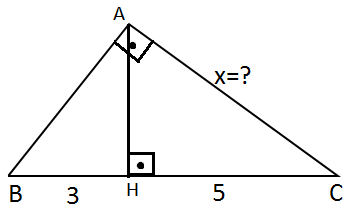
Yukarıdaki şekilde verilen x uzunluğunu hesaplayınız.