Epizykloide
Definition
Bisher haben wir immer Zykloiden betrachtet, die entstehen wenn ein Kreis auf einer
Geraden abrollt. Lässt man ihn hingegen auf einem anderem Kreis abrollen, so erhalten
wir eine weitere Spezialform der Zykloide, die Epizykloide.
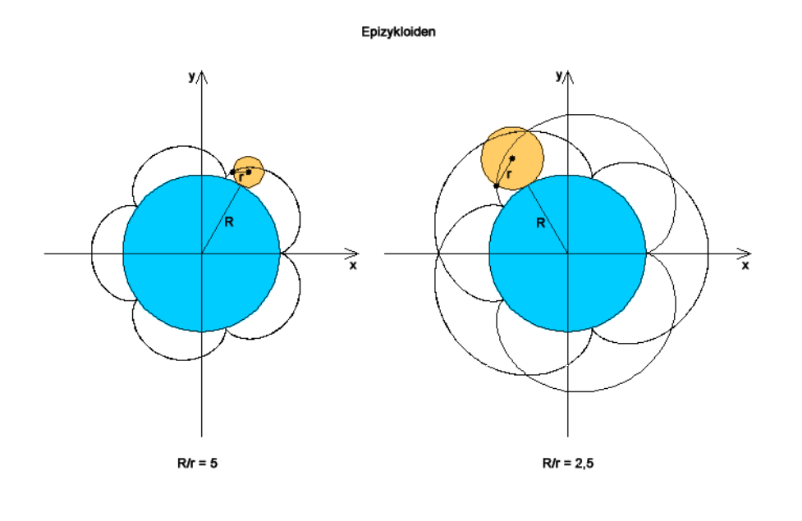
![[size=150]In der Mathematik werden beide Kurven häufig als Epizykloide bezeichnet, da sich die entstandene Kurve entweder durch das Abrollen eines Kreises auf einem anderen Kreis und auch durch das Abrollen eines Kreises um einen Kreis erzeugen lässt. Diese Erkenntnis wird zweifacher Erzeugung von Zykloiden genannt.[/size]](https://www.geogebra.org/resource/hqk7kdwv/TcR6qxr2c2p02lEs/material-hqk7kdwv.png)
![[size=150]Spezielle Epizykloiden:
[list][*]Für [b][i]i[/i] = 1[/b] ergibt sich die Herzkurve ([url=https://de.wikipedia.org/wiki/Kardioide]Kardioide[/url])[/*][/list][/size]](https://www.geogebra.org/resource/wjzfgu63/fV5m81uBmrGpDcIM/material-wjzfgu63.png)
- Für i = 1 ergibt sich die Herzkurve (Kardioide)