Das Steigungsdreieck
Einführung
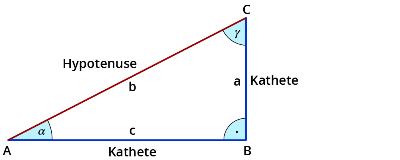
Begriffe im rechtwinkligen Dreieck
Bewegen des Punktes B
Bewege den Punkt B auf dem Graphen. Was kannst du feststellen?
Beide Punkte bewegen
Du darfst nun beide Punkte bewegen. Stelle den Punkt A auf die Koordinaten (1|1,5) und den Punkt B auf die Koordinaten (2|2). Berechne nun den Quotienten aus der Länge der senkrechten Kathete und der Länge der waagerechten Kathete und trage das Ergebnis ein:
Stelle nun Punkt A auf (0|1) und belasse B an seinem Ort. Berechne erneut den Quotienten:
Nun tauschen wir A und B: B(-2|0) und A(4|3). Du siehst, dass die Pfeile ihre Richtung ändern. Zeigen sie nach links bzw. unten nehmen die Kathetenlängen negative Werte an. Welchen Wert hat der Quotient nun?
Diesen Wert, den du gerade bestimmt hast, nennt man Steigung des Graphen. Du kennst ihn bereits aus der Funktionsgleichung . Du hast nun alle Informationen, um die Funktionsgleichung des Graphen zu bestimmen. Trage sie ins Antwortfeld ein. Vergiss den y-Achsenabschnitt nicht!
Fallende Geraden
Wir haben bereits erarbeitet, dass die Steigung negativ sein muss, wenn der Graph fällt. Ermittle mit dem gleichen Quotienten die Steigung dieses Graphen. Achte darauf, dass nun einer der beiden Pfeile einen negativen Wert hat. Wähle zwei Positionen für A und B und berechne dann die Steigung:
Wir sehen also, dass die Steigung negativ ist. Bilde nun für diesen Graphen die Funktionsgleichung und trage sie ein: