Maanrakennus
![Kuva [url=https://pixabay.com/fi/users/ritae-19628/?utm_source=link-attribution&utm_medium=referral&utm_campaign=image&utm_content=2464761]RitaE[/url] [url=https://pixabay.com/fi/?utm_source=link-attribution&utm_medium=referral&utm_campaign=image&utm_content=2464761]Pixabaystä[/url]](https://www.geogebra.org/resource/mytwqtsr/aWxd5PZoCW8TTJ3z/material-mytwqtsr.png)
Maanrakennustyömaalle tarvitaan vähintään 200 m3 hiekan ja soran seosta. Seoksessa
saa olla enintään 100 m3 hiekkaa ja siinä on oltava vähintään 120 m3 soraa. Hiekan ja
soran seosta on mahdollista saada kahdesta eri paikasta. Paikasta 1 on saatavilla hiekan
ja soran sekoitusta, jossa on 30 % hiekkaa ja 70 % soraa hintaan 7 e/m3 ja paikasta
2 sekoitusta, jossa on jossa on 60 % hiekkaa ja 40 % soraa hintaan 5 e/m3. Kuinka
paljon hiekan ja soran seosta tulisi toimittaa paikasta 1 ja kuinka paljon paikasta 2, jotta
kustannukset minimoituisivat?
Ratkaisu
Muodostetaan kustannuksia kuvaava funktio ja ongelmaa rajoittavat epäyhtälöt ja ratkaistaan
kustannusminimi.
Merkitään:
x on hiekan ja soran seosmäärä paikasta 1
y on hiekan ja soran seosmäärä paikasta 2
Minimoitava kustannusfunktio on muotoa
Kokonaiskustannus siis koostuu hiekan ja soran seosmäärä paikasta 1 kerrottuna sen hinnalla (7x) plus hiekan ja soran seosmäärä paikasta 2 kerrottuna sen hinnalla (5y).
Mahdollisia hiekka-sora seoksen määriä rajaa epäyhtälöt:
Paikasta 1 olevan seoksen määrän x on oltava vähintään nolla.
Paikasta 2 olevan seoksen määrän y on oltava vähintään nolla.
) Hiekka-sora seosta on oltava vähintään 200 m3.
Soran kokonaismäärän on oltava vähintään 120 m3.
Epäyhtälöt toteutuvat tason pisteissä, jotka ovat:
suoralla x + y = 200 tai sen yläpuolella ()
suoralla 0,3x + 0,6y = 100 tai sen alapuolella ()
suoralla 0,7x + 0,4y = 120 tai sen yläpuolella ()
Piirretään suorat koordinaatistoon ja etsitään suorien leikkauspisteiden koordinaatit:
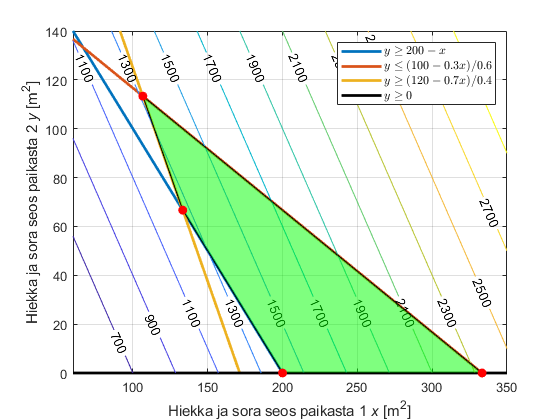
Määritetään kustannusfunktion z arvo suorien leikkauspisteissä:
z(200, 0) = 1400 e
z(133,33; 66,67) = 1266,7 e
z(106,67; 113,33) = 1313,3 e
z(333,33; 0) = 2333,3 e
Kustannukset ovat minimissään, kun hiekan ja soran seosta toimitetaan 134 m3
paikasta 1 ja 67 m3 paikasta 2.