Volume of a Sphere
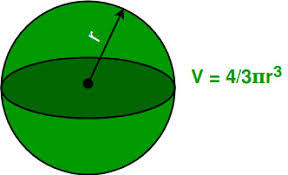
In three dimensions, the volume inside a sphere (that is, the volume of a ball, but classically referred to as the volume of a sphere) is:
where r is the radius and d is the diameter of the sphere. Archimedes first derived this formula by showing that the volume inside a sphere is twice the volume between the sphere and the circumscribed cylinder of that sphere (having the height and diameter equal to the diameter of the sphere).[6] This may be proved by inscribing a cone upside down into a semi-sphere, noting that the area of a cross-section of the cone plus the area of a cross-section of the sphere is the same as the area of the cross-section of the circumscribing cylinder, and applying Cavalieri's principle.[7] This formula can also be derived using integral calculus, i.e. disk integration to sum the volumes of an infinite number of circular disks of infinitesimally small thickness stacked side by side and centered along the x-axis from x = −r to x = r, assuming the sphere of radius r is centered at the origin. At any given x, the incremental volume (δV) equals the product of the cross-sectional area of the disk at x and its thickness (δx):
The total volume is the summation of all incremental volume:
In the limit as δx approaches zero, this equation becomes:
At any given x, a right-angled triangle connects x, y, and r to the origin; hence, applying the Pythagorean theorem yields: 
Using this substitution gives:
which can be evaluated to give the result
An alternative formula is found using spherical coordinates, with volume element{\displaystyle dV=r^{2}
so:
For most practical purposes, the volume inside a sphere inscribed in a cube can be approximated as 52.4% of the volume of the cube, since V = π/6 d3, where d is the diameter of the sphere and also the length of a side of the cube and π/6 ≈ 0.5236. For example, a sphere with a diameter of 1 m has 52.4% of the volume of a cube with edge length 1 m, or about 0.524 m3.
where r is the radius and d is the diameter of the sphere. Archimedes first derived this formula by showing that the volume inside a sphere is twice the volume between the sphere and the circumscribed cylinder of that sphere (having the height and diameter equal to the diameter of the sphere).[6] This may be proved by inscribing a cone upside down into a semi-sphere, noting that the area of a cross-section of the cone plus the area of a cross-section of the sphere is the same as the area of the cross-section of the circumscribing cylinder, and applying Cavalieri's principle.[7] This formula can also be derived using integral calculus, i.e. disk integration to sum the volumes of an infinite number of circular disks of infinitesimally small thickness stacked side by side and centered along the x-axis from x = −r to x = r, assuming the sphere of radius r is centered at the origin. At any given x, the incremental volume (δV) equals the product of the cross-sectional area of the disk at x and its thickness (δx):
The total volume is the summation of all incremental volume:
In the limit as δx approaches zero, this equation becomes:
At any given x, a right-angled triangle connects x, y, and r to the origin; hence, applying the Pythagorean theorem yields: Using this substitution gives:
which can be evaluated to give the result
An alternative formula is found using spherical coordinates, with volume element{\displaystyle dV=r^{2}so:
For most practical purposes, the volume inside a sphere inscribed in a cube can be approximated as 52.4% of the volume of the cube, since V = π/6 d3, where d is the diameter of the sphere and also the length of a side of the cube and π/6 ≈ 0.5236. For example, a sphere with a diameter of 1 m has 52.4% of the volume of a cube with edge length 1 m, or about 0.524 m3.