Definizioni e teoremi
Una corda è un segmento che congiunge due qualsiasi punti di una circonferenza.
Una corda che passa per il centro della circonferenza si dice diametro.
Gli estremi di un diametro si dicono diametralmente opposti.
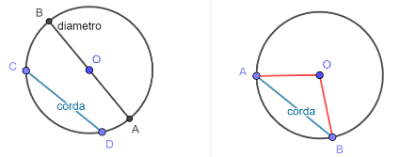
Teorema: Corde e diametri
Il diametro è una corda di lunghezza massima.
oppure
Ogni corda non passante per il centro è minore del diametro.
Dimostrazione
Una corda AB non passante per il centro O individua un triangolo isoscele. Basta congiungere gli estremi della corda con il centro della circonferenza (operazione che vi conviene tenere a mente quando dovete eseguire qualche dimostrazione).
Applicando la disuguaglianza triangolare al lato AB del triangolo ABO, abbiamo che AB < OA + OB.
Dato che la lunghezza di OA + OB = lunghezza del diametro, possiamo dire che la corda è minore del diametro.
Teorema: L'asse di una corda passa per il centro della circonferenza.
Ipotesi: AB è una corda ed O è il centro della circonferenza
Tesi: O appartiene all'asse di AB
Dimostrazione
Dato che O è equidistante da A e B perchè è il centro della circonferenza, O deve appartenere all'asse di AB (che è il luogo dei punti equidistanti da A e da B; quindi, tutti i punti equidistanti da A e da B devono appartenere all'asse di AB).
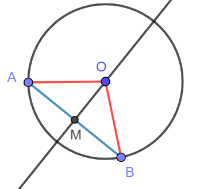
Teorema: La perpendicolare a una corda passante per il centro è l'asse della corda
Ipotesi: r è una retta perpendicolare alla corda AB, O è il centro della circonferenza, O r
Tesi: r è l'asse di AB
Dimostrazione
- M sia il punto di intersezione tra r e AB.
- Il triangolo ABO è isoscele, dato che OA e OB sono raggi della stessa circonferenza.
- OM è l'altezza del triangolo AOB perchè OM è perpendicolare ad AB per ipotesi.
- OM è anche mediana perchè in un triangolo isoscele altezza e mediana coincidono; quindi, M è il punto medio di AB.
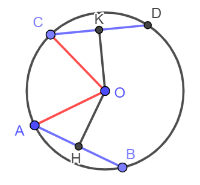
Teorema: relazioni tra corde congruenti e relativa distanza dal centro
In una circonferenza (o in circonferenze congruenti) se due corde sono congruenti, allora hanno la stessa distanza dal centro.
Ipotesi: AB e CD sono corde, AB CD, OH AB, OK CD
Tesi: OH OK
Dimostrazione
Per il teorema che afferma che la perpendicolare a una corda passante per il centro è l'asse della corda, possiamo dire che H e K sono i punti medi delle corde AB e CD.
Pertanto, AH CK perchè sono la metà di segmenti congruenti.
I triangoli AOH e COK sono rettangoli (perchè il segmento della distanza è perpendicolare); inoltre:
OA OC perchè sono raggi
AH CK perchè sono la metà di segmenti congruenti.
Quindi, i triangoli AOH e COK sono congruenti per il criterio dei triangoli rettangoli (caso particolare ipotenusa e cateto).
Di conseguenza, OH OK perchè sono elementi corrispondenti in triangoli congruenti.
Teorema (inverso)
Se due corde hanno la stessa distanza dal centro, sono congruenti.
Ipotesi: OH OK
Tesi: AB CD
Dimostrazione
I triangoli rettangoli AOH e COK sono congruenti perchè hanno l'ipotenusa e un cateto congruenti, dato che AO OC perchè sono raggi e OH OK per ipotesi. Pertanto, AH CK perchè sono elementi corrispondenti in triangoli congruenti. Di conseguenza anche AB CD, dato che H e K sono i punti medi delle corde.
Teorema
Se due corde di una circonferenza (o di circonferenze congruenti) non sono congruenti, allora la corda minore ha distanza dal centro maggiore dell'altra.
Tralasciamo la dimostrazione di questo teorema, per il momento.
Prova a modificare la lunghezza delle corde e osserva come cambia la loro distanza dal centro
Teorema "riassuntivo" sulle corde e la loro distanza dal centro
Se AB e CD sono due corde di una circonferenza di centro O,
- AB CD se e solo se la distanza di AB da O è congruente alla distanza di CD da O
- AB < CD se e solo se la distanza di AB da O è maggiore della distanza di CD da O
- AB > CD se e solo se la distanza di AB da O è minore della distanza di CD da O