Ekuazio linealak ebazten
1. Linear Equations
Ekuazio hauek lineal gisa ezagutzen dira, zati literal monomialak ez duelako adierazlerik (adibidez, 3x ekuazio lineal baten zati izan daiteke, baina 3x2 ezin da izan, koadratikoa delako), eta, beraz, grafiko batean lerro gisa agertzen da. Honek soluzio bat baldin badago soluzio bakarra izan daitekeela ziurtatzen digu (kasu berezietan amaigabeak izan ezik).
Konponbiderik ba ote dagoen esaten dugu, batzuetan ekuazioek ez dutelako konponbiderik. Adibidez, x = x + 1 ekuazioak (zenbaki batek hurrenez hurreneko zenbakiaren berdina esan nahi du) ez du soluziorik, hau ez baita inoiz egia. Izan ere, ekuazio hori 1 = 0ra murrizten da, eta hori ezinezkoa da.
Pistak
- Ezinezko berdintasuna lortzen badugu, ez dago konponbiderik, 1 = 0 bezala.
- Beti egia den berdintasun bat lortzen badugu, edozein baliok konponbidea ematen duela ere, orduan konponbidea zenbaki errealak dira. Adibidez, 0 = 0 lortzen badugu.
- Izendatzaileak daudenean eta saihestu nahi ditugunean, ekuazio osoa biderkatu egiten dugu izendatzaileen multiplo komun txikienarekin. Horrela, sinplifikatzen garenean, desagertu egiten dira.
- Parentesia kentzeko, bere aurrean dagoen koefizientea biderkatzen dugu dituen elementu guztiekin. Koefiziente hori zeinu negatibo bat izan daiteke (adibidez, 1, edukia zeinuz aldatzen da), zeinu positibo bat (+1, edukia ez da aldatzen) edo zenbaki edo frakzio positibo edo negatibo bat (zenbaki horrek dena biderkatzen du parentesi artean, zeinuak aldatuz bere negatiboa bada).
- Parentesi habiatu bat dugunean, parentesi bat beste parentesi baten barruan, kanpotik barrura ateratzeko erregutzen dugu. Lehenik, kanpoko parentesia kentzen dugu (edukia koefizienteekin biderkatuz) eta, ondoren, gainerakoa era berean kentzen dugu, kanpokoenetik barnekoenera.
1.Adibidea
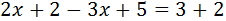
Gehitu (edo kendu) monomialak zati literalean (x 's x' rekin eta zenbakiak zenbakiekin). Alde batetik gehitzen dena, beste aldetik kentzen da, eta alderantziz.
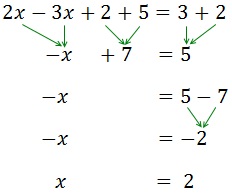
Gero, X-a berdintasunaren alde batean jartzen dugu, eta zenbakiak bestean.
Gehitu (edo kendu) monomialak zati literalean (x 's x' rekin eta zenbakiak zenbakiekin). Alde batetik gehitzen dena, beste aldetik kentzen da, eta alderantziz.
Gero, X-a berdintasunaren alde batean jartzen dugu, eta zenbakiak bestean.
2.adibidea
2.adibidea
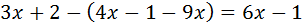
Lehenik, parentesia kenduko dugu: aurrean zeinu negatiboa duenez, ausaz barneko elementu guztien zeinua.
Gero, X-a alde batean eta zenbakiak bestean multzokatzea besterik ez da falta.
Lehenik, parentesia kenduko dugu: aurrean zeinu negatiboa duenez, ausaz barneko elementu guztien zeinua.
Gero, X-a alde batean eta zenbakiak bestean multzokatzea besterik ez da falta.
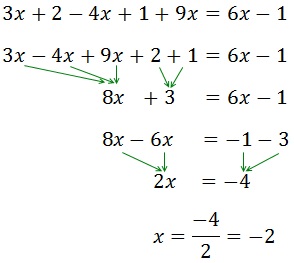
Izan ere, X-k koefiziente bat du, 2, hau da, biderkatu egiten da, eta beste aldera mugitzen da, zatituz.
Ebatzitako adibide gehiago:
Izan ere, X-k koefiziente bat du, 2, hau da, biderkatu egiten da, eta beste aldera mugitzen da, zatituz.
Ebatzitako adibide gehiago:
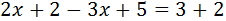
Gehitu (edo kendu) monomialak zati literalean (x 's x' rekin eta zenbakiak zenbakiekin). Alde batetik gehitzen dena, beste aldetik kentzen da, eta alderantziz.
Gero, X-a berdintasunaren alde batean jartzen dugu, eta zenbakiak bestean.
Gehitu (edo kendu) monomialak zati literalean (x 's x' rekin eta zenbakiak zenbakiekin). Alde batetik gehitzen dena, beste aldetik kentzen da, eta alderantziz.
Gero, X-a berdintasunaren alde batean jartzen dugu, eta zenbakiak bestean.

2.adibidea
2.adibidea
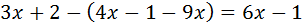
Lehenik, parentesia kenduko dugu: aurrean zeinu negatiboa duenez, ausaz barneko elementu guztien zeinua.
Gero, X-a alde batean eta zenbakiak bestean multzokatzea besterik ez da falta.
Lehenik, parentesia kenduko dugu: aurrean zeinu negatiboa duenez, ausaz barneko elementu guztien zeinua.
Gero, X-a alde batean eta zenbakiak bestean multzokatzea besterik ez da falta.
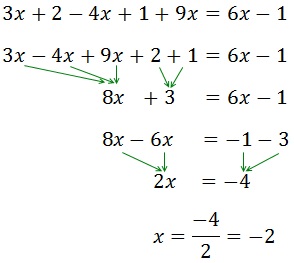
Izan ere, X-k koefiziente bat du, 2, hau da, biderkatu egiten da, eta beste aldera mugitzen da, zatituz.
Ebatzitako adibide gehiago:
Izan ere, X-k koefiziente bat du, 2, hau da, biderkatu egiten da, eta beste aldera mugitzen da, zatituz.
Ebatzitako adibide gehiago: