Singular Value Decomposition (SVD)
Θέλουμε να διαγωνιοποιήσουμε έναν τετραγωνικό πίνακα A αλλά όχι μέσω της σχέσης X-1AX = L .
Έστω δύο σύνολα ιδιαζουσών διανυσμάτων
u=(u1,u2,...,ur) και v=(v1,v2,...,vr) όπου r είναι η τάξη του πίνακα A. Οι συνιστώσες του διανύσματος u, ανήκουν στο χώρο στηλών του A και αποτελούν τα ιδιοδιανύσματα του πίνακα AAT ενώ οι συνιστώσες του v ανήκουν στο χώρο γραμμών του A και αποτελούν τα ιδιοδιανύσματα του ATA. Οι πίνακες AAT και ATA είναι και οι δύο συμμετρικοί, και τα ιδιοδιανύσματα τους μπορούν να θεωρηθούν ορθοκανονικά δηλαδή να έχουν μηδενικό εσωτερικό γινόμενο. Ισχύει οι σχέση AV = UΣ .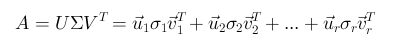
Δοθέντος του τετραγωνικού πίνακα A υπολογίζω τον ανάστροφο AT και στη συνέχεια το γινόμενο των δύο πινάκων ATA. Στη συνέχεια της λύσης ως πίνακας θεωρείται ο Α = [{2,2}; {-1,1}].
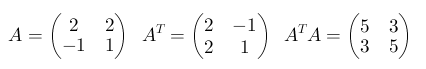
Στη συνέχεια υπολογίζουμε τα ιδιοδιανύσματα του πίνακα ATA και κάνουμε κανονικοποίηση αυτών.
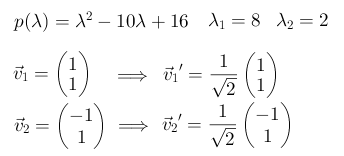
Βρίσκουμε τις θετικές τιμές του διαγώνιου πίνακα Σ μέσω των ιδιοτιμών του ATA.
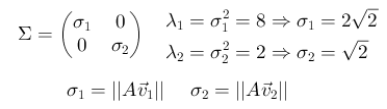
Υπολογίζουμε τα διανύσματα u μέσω των Av που βρίσκονται στην κατεύθυνση των u.
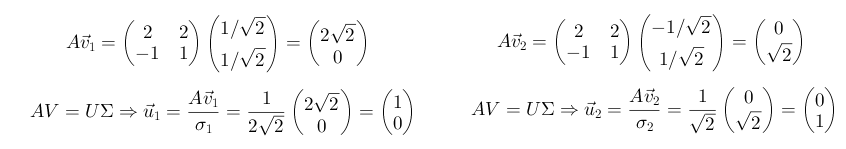
Σημείωση : Μπορούμε να υπολογίσουμε τα διανύσματα u από τα v. Όμως μπορούμε και απευθείας από το γινόμενο AAT και όχι από το ΑΤΑ. Τα διανύσματα u τότε, είναι τα ιδιοδιανύσματα του πίνακα AAT.
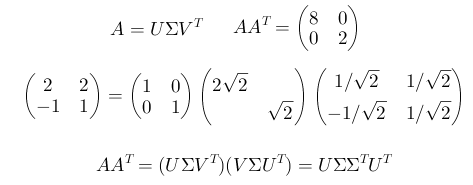
Τελικά από τα παραπάνω προκύπτει ότι οι singular values είναι οι και .