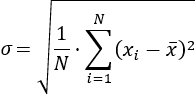Parámetros (estadística básica)
1. Introducción
Un parámetro de una población es una medida que resume o describe el comportamiento general de dicha población.
Vamos a dar algunos parámetros (de centralización y de dispersión) y a explicar cómo calcularlos mediante un ejemplo.
2. Parámetros de centralización
Son las medidas que informan acerca de la mayor o menor agrupación o concentración de los datos entorno a la media: media, moda y mediana.
Supongamos que queremos estudiar la altura (en centímetros) de un grupo de 10 alumnos de un aula:
165, 170, 175, 173, 169,
183, 171, 176, 172, 170
Si observamos todos los datos, encontramos alturas muy cercanas (como 170, 171, 172 y 173) y otras muy lejanas (como 165 y 183). Pero podemos decir, por simple observación, que la mayoría ronda o se aproxima a los 173cm.
En estadística, esta altura aproximada se denomina media y se calcula sumando todas las alturas y dividiendo el resultado entre el número total de alturas (es el promedio o la media aritmética):
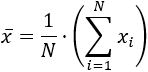
Calculamos la media de las alturas del ejemplo:
Calculamos la media de las alturas del ejemplo:
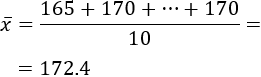
Hay otros aspectos que nos importan de la población, por ejemplo:
Hay otros aspectos que nos importan de la población, por ejemplo:
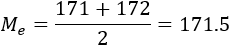
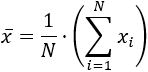
Calculamos la media de las alturas del ejemplo:
Calculamos la media de las alturas del ejemplo:
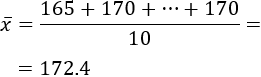
Hay otros aspectos que nos importan de la población, por ejemplo:
Hay otros aspectos que nos importan de la población, por ejemplo:
- ¿Cuál es la altura que más se repite?
- ¿Hay más alturas por debajo de la media o por encima?
- ¿Hay mucha diferencia entre las alturas y la altura media?
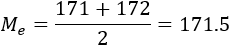
3. Parámetros de dispersión
Son los parámetros que indican la mayor o menor concentración de los datos alrededor de los parámetros de centralización: desviación respecto de la media, desviación media, varianza y desviación estándar.
Si tomamos un dato, , su desviación respecto de la media es la diferencia entre ellos (en valor positivo). Es decir,
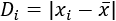
La desviación media es la media de todas las desviaciones respecto de la media. Es decir, se suman todas las desviaciones (hay N) y se divide entre el número de datos (N):
La desviación media es la media de todas las desviaciones respecto de la media. Es decir, se suman todas las desviaciones (hay N) y se divide entre el número de datos (N):
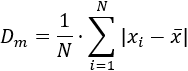
Calculamos las desviaciones y la desviación media de nuestro ejemplo:
Calculamos las desviaciones y la desviación media de nuestro ejemplo:
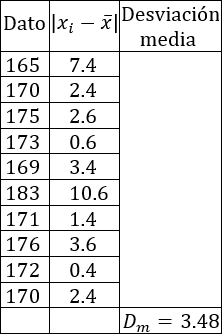
La desviación media es 3.18. La traducción de este dato es que la media de las diferencias de cada altura con la altura media es 3.18cm.
Si la desviación media es muy grande, entonces las alturas de los alumnos varían mucho de la media. Mientras que si es muy pequeña, varían poco.
La varianza o variancia es
La desviación media es 3.18. La traducción de este dato es que la media de las diferencias de cada altura con la altura media es 3.18cm.
Si la desviación media es muy grande, entonces las alturas de los alumnos varían mucho de la media. Mientras que si es muy pequeña, varían poco.
La varianza o variancia es
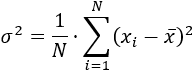
La desviación típica es la raíz cuadrada de la varianza:
La desviación típica es la raíz cuadrada de la varianza:
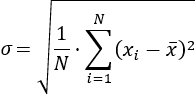
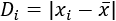
La desviación media es la media de todas las desviaciones respecto de la media. Es decir, se suman todas las desviaciones (hay N) y se divide entre el número de datos (N):
La desviación media es la media de todas las desviaciones respecto de la media. Es decir, se suman todas las desviaciones (hay N) y se divide entre el número de datos (N):
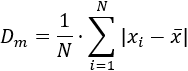
Calculamos las desviaciones y la desviación media de nuestro ejemplo:
Calculamos las desviaciones y la desviación media de nuestro ejemplo:

La desviación media es 3.18. La traducción de este dato es que la media de las diferencias de cada altura con la altura media es 3.18cm.
Si la desviación media es muy grande, entonces las alturas de los alumnos varían mucho de la media. Mientras que si es muy pequeña, varían poco.
La varianza o variancia es
La desviación media es 3.18. La traducción de este dato es que la media de las diferencias de cada altura con la altura media es 3.18cm.
Si la desviación media es muy grande, entonces las alturas de los alumnos varían mucho de la media. Mientras que si es muy pequeña, varían poco.
La varianza o variancia es
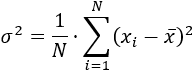
La desviación típica es la raíz cuadrada de la varianza:
La desviación típica es la raíz cuadrada de la varianza: