Atividade IV - Parte 02 - Questões de Funções Trigonométricas
Questão 01 - Cálculo da largura do rio.
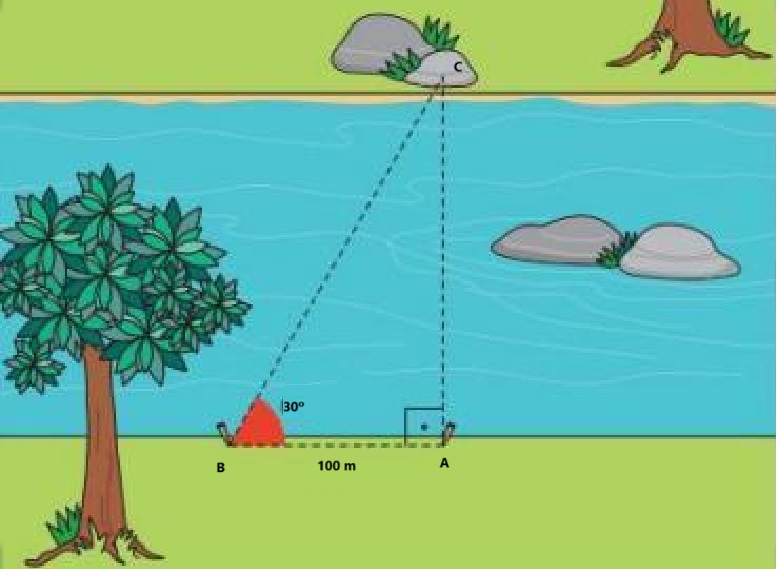
Para determinar a largura de um rio, determino-se a distância entre dois pontos A e B de uma margem: AB = 100 m. Numa perpendicular às margens pelo ponto A visou-se um ponto C na margem oposta e se obteve o ângulo m(ABC)=30º. Calcule a largura do rio.
No espaço abaixo, insira uma foto da resolução dessa questão, feita à mão por voçê.
Questão 02 - Comprimento da sombra de uma arvore.
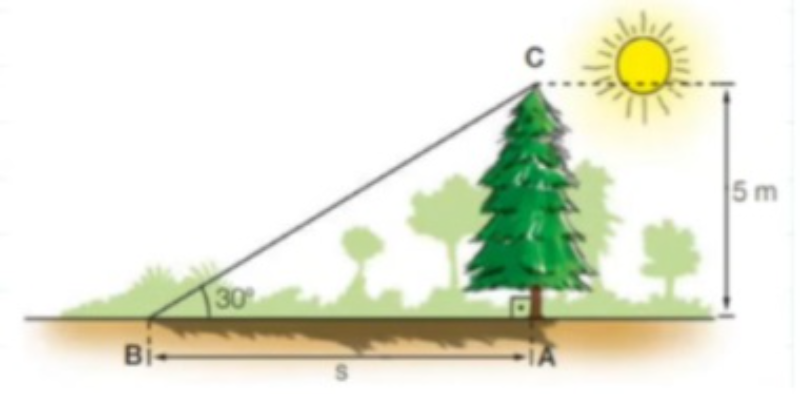
Qual o comprimento da sombra de uma arvore de 5m de altura quando o Sol está 30º acima do horizonte?
Questão 03 - Cálculo de um edificio.
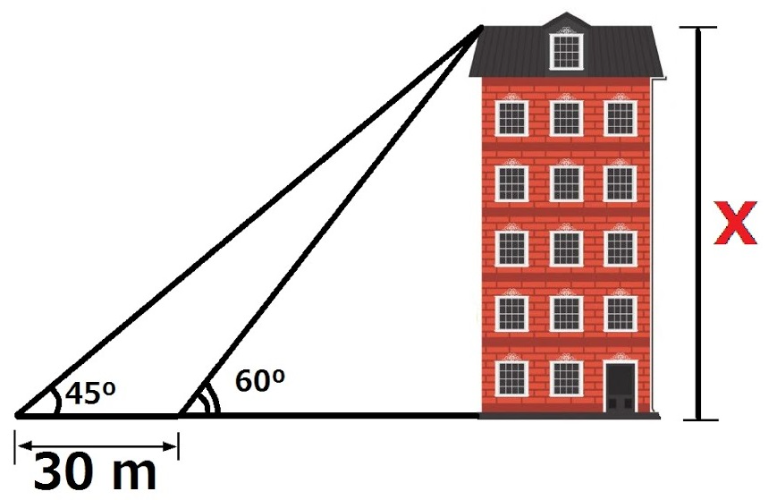
Um observador vê um edifício constrído em terreno plano, sob um ângulo de 60º. Se ele se afastar do edifício mais 30 m, passará a vê-lo sob um ângulo de 45º.
Calcule a altura do edifício.
No espaço abaixo, insira uma foto da resolução dessa questão, feita à mão por voçê.
Questão 04 - Calculo de perímetro.
No retângulo ABCD, AD=1, P está em AB e DB e DP dividem o ângulo ADC em três iguais. Qual o perímetro do triângulo BDP?
Questão 05 - Compreender os conceitos de seno, cosseno e tangente no triângulo retângulo.
Movimente os pontos B e E (em vermelho) e:
a) Observe o que acontece.
b) Observe a variação de valores dos segmentos de reta.
c) O qua acontece quando aumentamos o ângulo .
Descreva em poucas palavras as suas observações.
Questão 06 - Círculo Trigonométrico
Assista o vídeo e resolva as perguntas abaixo,
Círculo Trigonométrico
Desenrolando o círculo trigonométrico.
Após observar o desenrolar do círculo trigonométrico (aperte o Botão Play), responda as perguntas conforme orientação.
a) O que representa mover o Ponto P ao longo do eixo x?