I Teoremi di Euclide e Pitagora
Definizioni base
Per questi teoremi utilizzeremo un triangolo speciale, detto rettangolo.
Il triangolo rettangolo è un triangolo in cui due lati formano un angolo retto ().
I lati che formano un angolo retto sono detti cateti e li indicherò con e .
Il terzo lato, che è anche il più lungo, si chiama ipotenusa e la indicherò con .
L'altezza è un segmento che, partendo dal vertice, forma un angolo di con il lato opposto.
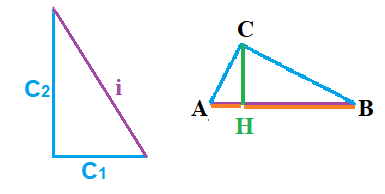
Presa l'altezza relativa all'ipotenusa e il punto dato dall'intersezione tra le due, si osserva che l'ipotenusa viene divisa in due segmenti. Questi prendono il nome di proiezione del cateto sull'ipotenusa. Rispetto alla figura sottostante:
- è la proiezione di su ;
- è la proiezione di su .
Teorema di Pitagora
Secondo il teorema di Pitagora, dato un triangolo rettangolo aventi cateti e ed ipotenusa , allora il quadrato costruito sull'ipotenusa è uguale alla somma dei quadrati costruiti sui cateti.
COSA SIGNIFICA? A livello di risoluzione si scrive così: .
Osservazione: quindi, se volessi calcolare il valore dell'ipotenusa, devo porre entrambi i membri sotto radice quadrata e ottengo .
Se volessi invece uno dei cateti devo "isolarlo" (ovvero portare al membro opposto l'altro cateto, si veda formule inverse) e poi porre entrambi i membri sotto radice .
Primo Teorema di Euclide
Sia ora il triangolo rettangolo con angolo retto in .
Sia anche l'altezza relativa all'ipotenusa , i triangoli e sono anche loro rettangoli.
Secondo il teorema di Euclide il quadrato costruito sul cateto ha area pari a quella del rettangolo che ha per dimensioni l'ipotenusa e la proiezione[1] del cateto sull'ipotenusa.
COSA SIGNIFICA? Ciascun cateto è medio proporzionale tra l'ipotenusa e la proiezione del cateto sull'ipotenusa.
AB : CB = CB : HB AB : AC = AC : AH
A livello di risoluzione si scrivono così: e .Secondo Teorema di Euclide
Sia ora il triangolo rettangolo con angolo retto in .
Sia anche l'altezza relativa all'ipotenusa , i triangoli e sono anche loro rettangoli.
Secondo il secondo teorema di Euclide il quadrato costruito sull'altezza relativa all'ipotenusa ha area pari a quella del rettangolo che ha per dimensioni le proiezioni[1] dei cateti sull'ipotenusa.
COSA SIGNIFICA? L'altezza è medio proporzionale tra le proiezioni dei cateti sull'ipotenusa.
AH : CH = CH : HB
A livello di risoluzione si scrive così: .