Gradients
The gradient of a straight line
You are probably familiar with the idea of the gradient in the context of straight lines. You may be familiar with the formula , using to represent the change in y and to represent the change in x. Alternatively, we may have used . You should also be able to find the gradient of a straight line from its equation.
In each of the five questions below try to identify the gradient of the line.
Line 1
Line 2
Line 3
Line 4
Line 5
Gradients of other functions
But what if the equation is not a straight line. Below is a picture of a parabola, what does it mean to talk about the gradient of this function. We cannot just give a number anymore, take a moment to think about how you would describe the steepness of the parabola to somebody and write it below.
A parabola
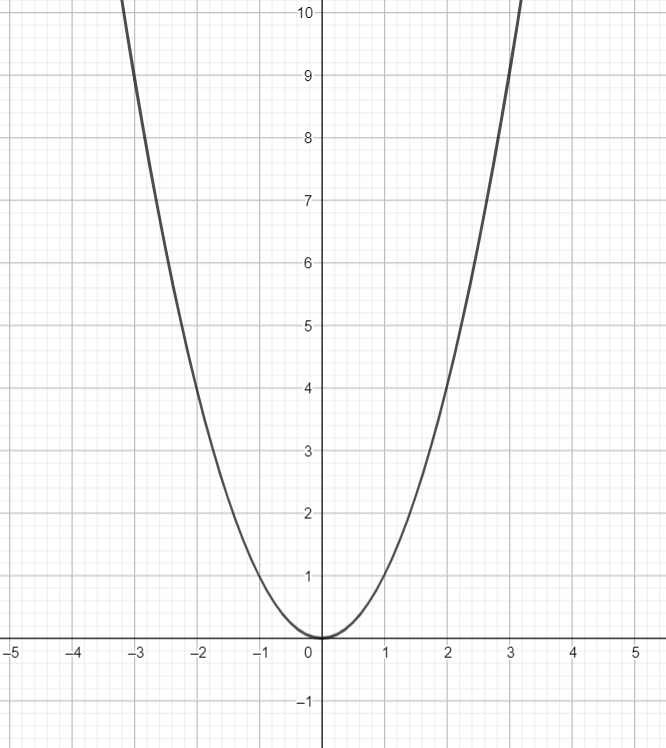
One option would be to describe the gradient at different points on the curve. For example,
"...on the left the curve is steep and the gradient is negative, as we move to the middle of the parabola the graph gets less steep until the origin when it is flat. Then the curve gets steeper again as we go to the right and the gradient is positive (the graph slopes upwards)..."
This is in fact what we are going to do. In order to do this we need to introduce the concept of a tangent to a function. The next task will let you explore tangents to different functions.