Grundlegendes
Voraussetzungen
Der Erfolg im 3. Semester ist an mathematische Voraussetzungen gebunden, die entweder in den Semestern 1 und 2 erworben wurden, oder die Sie aufgrund Ihres Abschlusses mitbringen. Nachfolgend finden Sie eine kurze Übersicht mit Erklärungen.
Die grundlegenden arithmetischen Rechenverfahren müssen Sie in allen Zahlbereichen beherrschen.
Das Wort Arithmetik kommt von Zählen, somit sind mit den grundlegenden arithmetischen Rechenverfahren die sogenannten Grundrechenarten gemeint.
Dabei ist das 'Kleine Einmaleins' durchaus hilfreich.
Der Begriff Zahlbereich ist möglicherweise etwas ungewohnt. Gemeint ist folgendes:
Sofern Sie nur positive Zahlen benutzen und auch nur abzählbare Objekt haben, rechnen Sie mit den natürlichen Zahlen. (0; 1; 2; 3; ...)
Im zweiten Semester haben Sie diese Zahlen, die am Zahlenstrahl angeordnet sind, am Nullpunkt gespiegelt. Damit haben Sie negative Zahlen erzeugt, und am Beispiel von Temperaturskalen, Höhenunterschieden und Kontoständen in die Mathematik eingebunden. Diesen Zahlreich nennen die Mathematiker den Bereich der ganzen Zahlen.
Im ersten Semester haben Sie die Bruchzahlen kennengelernt, sowohl als Dezimalzahlen, als auch als gemeine Brüche. Sie sollten sich im 3. Semester daran gewöhnen, mit den gemeinen Brüchen zu operieren, und nicht in der Dezimalzahlwelt verharren. Um gleich mit einem weit verbreiteten Irrtum aufzuräumen:ist nicht dasselbe wie 0,3!!!
(Das durchgestrichene Gleichheitszeichen bedeutet ungleich!)
Die Brüche nenne die Mathematiker rationale Zahlen.
Bei der Kreisberechnung haben Sie eine ganz besondere Zahl kennengelernt, die Zahl Pi ()
Sie ist weder rational, noch ganz, noch natürlich, aber man kann Sie auf dem Zahlenstrahl finden, deshalb ist es eine reelle Zahl, der Zahlreich, in dem Sie jetzt im 3. Semester angekommen sind.
Sie werden im dritten Semester auch noch die Quadratwurzeln kennenlernen werden, die zwar reell aber nur selten rational oder ganzzahlig sind. Dazu später mehr.
Nach diesem kurzen Überblick folgen nun die Grundlegenden Eigenschaften der Grundrechenarten.
Addition und Subtraktion
Die Rechenzeichen der Addition und Subtraktion bestehen aus Strichen, weshalb sie Strichrechnungen genannt wird.
Das Wichtigste auf einen Blick
Wie man die Strichrechnung mit Vektoren beschreibt, können Sie mit der nachfolgenden Datei ausprobieren.
Da die Subtraktion eine andere Richtung hat als die Addition, sind diese Operationen gegenseitige Umkehroperationen. Diesen Zusammenhang benötigen Sie später beim Gleichungslösen.
| | Addition | Subtraktion |
| Rechenzeichen | + (plus) | - (minus) |
| Ergebnis | Summe(nwert) S | Differenz(enwert) D |
| Eigenschaft | Summanden vertauschbar | Minuend und Subtrahend nicht vertauschbar |
| algebraische Darstellung | s1 + s2 = S | m - s = D |
Strichrechnung üben
Multiplikation und Division
Die Rechenzeichen der Multiplikation und der Division bestehen aus Punkten, weshalb sie Punktrechnungen genannt werden.
Das Wichtigste auf einen Blick
| | Multiplikation | Division |
| Rechenzeichen | mal (bitte kein x) | : 'geteilt durch' (auch Bruchstrich) |
| Ergebnis | Produkt(wert) P | Quotient(enwert) Q |
| Eigenschaften | Faktoren vertauschbar | Dividend (Zähler) und Divisor (Nenner) nicht vertauschbar |
| algebraische Darstellung | f1 f2 = P | z : n = Q auch |
Die Grundrechenarten mit Brüchen
Punktrechnung
Für die Punktrechnung gelten zwei Regeln:
1. Multiplikation
Zwei Brüche werden multipliziert, in dem jeweils die Zähler und die Nenner multipliziert werden!
2. Division
Zwei Brüche werden dividiert, indem der Bruch DIVIDENT mit dem Kehrwert des Bruches DIVISOR multipliziert wird.
Als Kehrwert wird ein Bruch bezeichnet, bei der Zähler zum Nenner wird und der Nenner zum Zähler.
Bruch: Kehrwert:
Strichrechnung
Für die Strichrechnung gilt nur eine einzige Regel:
Man kann Brüche nur addieren oder subtrahieren, wenn der Nenner der Summanden oder vom Bruch Minuend und Bruch Subtrahend gleich sind.
Dann werden die Zähler addiert bzw. subtrahiert, und der Nenner beibehalten.
Doch was macht man, wenn die Zähler nicht gleich sind?
Brüche sind "Zauberzahlen", sie können sich verwandeln, ohne dass sich ihr Wert ändert. Die mathematische Zauberformel lautet erweitern, bzw. kürzen.
Als erweitern bezeichnet man die Zauberformel:
Zähler und Nenner mit der gleichen Zahl multiplizieren.
Als kürzen bezeichnet man die Zauberformel:
Zähler und Nenner durch die gleiche Zahl zu dividieren.
Dafür benötigen Sie das 'Kleinen Einmaleins'.
Das Wort erweitern kommt daher, dass man Zähler und Nenner um einen gemeinsamen Faktor verlängert.
Das Wort kürzen kommt daher, dass man Zähler und Nenner um einen gemeinsamen Faktor verkürzt.
Hier finden Sie ein Buch zum Üben!
| Zahlenbeispiele | allgemeine Darstellung |
| | |
| Zahlenbeispiele | allgemeine Darstellung |
| | |
| | Zahlenbeispiel | allgemeine Darstellung |
| Addition | | |
| Subtraktion | | ist a < c wird der Bruch negativ |
| | Zahlenbeispiele | allgemeine Darstellung |
| erweitern | | |
| kürzen | | |
Rechenregeln
Beim Rechnen und beim Umformen gibt es einige Rechenregeln und Gesetze.
Das Vertauschungsgesetz wurde schon bei den Grundrechenarten erwähnt, dort durften Sie bei der Addition die Summanden und bei der Multiplikation die Faktoren vertauschen, ohne auf irgendetwas aufzupassen. Das Vertauschungsgesetz heißt in der Mathematik Kommutativgesetz.
Bei der Verknüpfung von zwei Rechenarten gibt es die Formulierung Punkt vor Strich, die streng genommen kein Gesetz ist, aber eine internationale Vereinbarung.
Das nachfolgende Applet gibt Ihnen die Möglichkeit, sich noch einem mit diesem Aspekt zu beschäftigen und sich auch daran zu erinnern, dass Klammerregeln eine wichtige Rolle spielen
Verknüpfung von zwei Rechenoperationen
Elementares Gleichungslösen
Das Lösen einer linearen Gleichung geht immer -zumindest in der Schule- auch durch probieren.
Das folgende Arbeitsblatt zeigt einige Aufgaben dazu.
Mit dem darunterliegenden Applet können Sie 10 unterschiedliche Gleichungen durch probieren lösen, bzw. im Kopf lösen.
02_Grundlagen
Kopfrechenübung
Weiterführende Ideen
Überzeugen Sie sich durch geeignete Zahlenbeispiele, dass auch bei der Verknüpfung mit der Division die Reihenfolge der Rechenoperationen -in der Regel- zu unterschiedlichen Ergebnissen führt.
Ihrer Aufmerksamkeit wird nicht entgangen sein, das in diesem Wiederholungskapitel die Formulierung -in der Regel- verwendet wird.
Vielleicht finden Sie heraus, wann -Mathematiker neben das den Spezialfall- die Rechenoperationen auch bei Nichtbeachtung der Regel 'Punkt vor Strich' gleiche Ergebnisse liefert.
Äquivalenzumformung
Im zweiten Semester haben Sie die Begriffe:
Term Termumformung Gleichung Gleichungsumformung
kennen und anwenden gelernt.
Das Ziel bestand darin, dass Sie Gleichungen nicht durch probieren lösen, sondern mit den Hilfen der Algebra. Algebra ist die Mathematik, in der statt Zahlen (Zahlsymbole) Buchstaben (Schriftsymbole) als Platzhalter für Zahlen verwendet werden. Der bekannteste Buchstabe ist das x.
Was ist...
Die Hinweis auf die gleiche Operation rechtfertigt den Begriff Äquivalenzumformung.
Das nachfolgende Applet zeigt das Waagemodell, das Sie dann erinnern soll, wie Sie eine Gleichung lösen.
Sind auf beiden Seiten des Gleichheitszeichens unterschiedliche Werte, so ist die Gleichung im Ungleichgewicht. Dann kann eine Seite größer als die andere Seite sein. In einem solchen Fall ist der Ausdruck eine Ungleichung.
Ungleichungen haben ein eigenes Zeichen:
< : die linke Seite vom Zeichen ist kleiner als die rechte Seite (13 < 77)
> : die linke Seite vom Zeichen ist größer als die rechte Seite (77 > 13)
| ... ein Term | Ein Term ist ein mathematischer Ausdruck, in dem zwei Zahlen (oder Buchstaben mit einem Rechenzeichen verknüpft sind. Das Rechenzeichen bestimmt den Termnamen. 13 + 7 ==> Summenterm (auch s + t) 6 •7 (auch a•b) 12 - 5 ==> Differenzterm (auch c - d) 17 : 5 ==> Quotiententerm (auch (e : f), |
| ... eine Termumformung | Bei Zahlen formen Sie einen Term schon um, wenn Sie den neuen Zahlenwert bestimmen: 13 + 7 ==> 20 6 •7 ==> 42 ... Wenn Sie Buchstaben verwenden, dann können Sie bei der Strichrechnung nur gleich Buchstaben zusammenfassen. Bei der Punktrechnung alle Buchstaben. a•b ==> ab ... |
| ... eine Gleichung | Eine Gleichung vergleicht zwei Terme und verlangt die Überprüfung, ob die beiden Terme gleich sind. Man nennt eine Gleichung auch Aussage. Aussagen können wahr (w) oder falsch (f) sein. Sind sie gleich, ist die Aussage wahr, ist sie falsch ist die Aussage falsch. 13 + 7 = 20 (w) 6•7 = 41 (f) |
| ... eine Gleichungsuformung | 13 + 7 = 20 <=== hier haben Sie die Gleichung umgeformt, und den Term durch einen einfacheren Term (1•20) ausgedrückt. In der Regel benutzen Sie jedoch die Gleichungsumformung, um eine Variable (meist x) zu bestimmen. 31 - x = 15 | + x 31 -x + x = 15 +x <=> 31 + 0 = 15 + x <=> 31 = 15 + x 31 = 15 + x | - 15 31 - 15 = x <=> 16 = x Dabei muss man immer auf beiden Seiten des Gleichheitszeichens dieselbe Operation ausführen. |
Gleichung im Waagemodell
Das Koordinatensystem
Das Hauptwerkzeug im 3. Semester ist die Verwendung eines Koordinatensystems, um Funktionen grafisch darzustellen. Die Idee des sogenannten kartesischen Koordinatensystems (KOS) geht auf auf René Descartes zurück und ist somit aus dem aus dem 17. Jahrhundert.
Grob gesprochen handelt es sich um zwei Geraden, die senkrecht aufeinander stehen. Dadurch entstehen vier Felder, die - aufgrund von Symmetrieüberlegungen quadratisch sein müssen - als Quadranten bezeichnet werden.
Die waagerechte Achse kann man als RECHTSACHSE bezeichnen (richtig heißt sie ABSZISSE, was von 'abgeschnittener Linie' kommt, ZAHLENSTRAHL) und die senkrechte Achse kann man als HOCHACHSE (richtig heißt sie ORDINATE, was von ordnen, bzw. ZUORDNEN kommt)
Wichtiger als diese Namen, ist jedoch die Unterscheidung:
unabhängig, was bedeutet, Sie können hier frei Werte wählen
und
abhängig, was bedeutet, dass dieser Wert von einer Definition (Funktionsterm) abhängt.
Prägen Sie sich das nachfolgende Bild gut ein. Sie können auch Punkte eintragen und sich anschauen, welche KOORDINATEN die Punkte haben. Der Schnittpunkt der Achsen wird in der Mathematik der URSPRUNG genannt, und hat die Koordinaten: O = (0|0)
Bei Anwendungsaufgaben muss das nicht so sein.
Allgemeine Koordinaten
Allgemeine Koordinaten sind Koordinaten, die gleiche Eigenschaften haben. Wenn Sie in der vorherigen Applikation den Punkt P auf der x - Achse platzieren, dann hat P die Koordinaten (0|x-Wert), wenn sie ihn auf der y-Achse platzieren die Koordinaten (y-Wert|0).
Punkte auf der x-Achse haben immer die als y-Wert den Wert 0. (Nullstelle)
Punkte auf der y-Achse haben immer als x - Wert den Wert 0. (Achsenabschnitt)
Damit wird deutlich, das Punkte im Koordinatensystem immer die allgemeine Form:
P = (x|y)
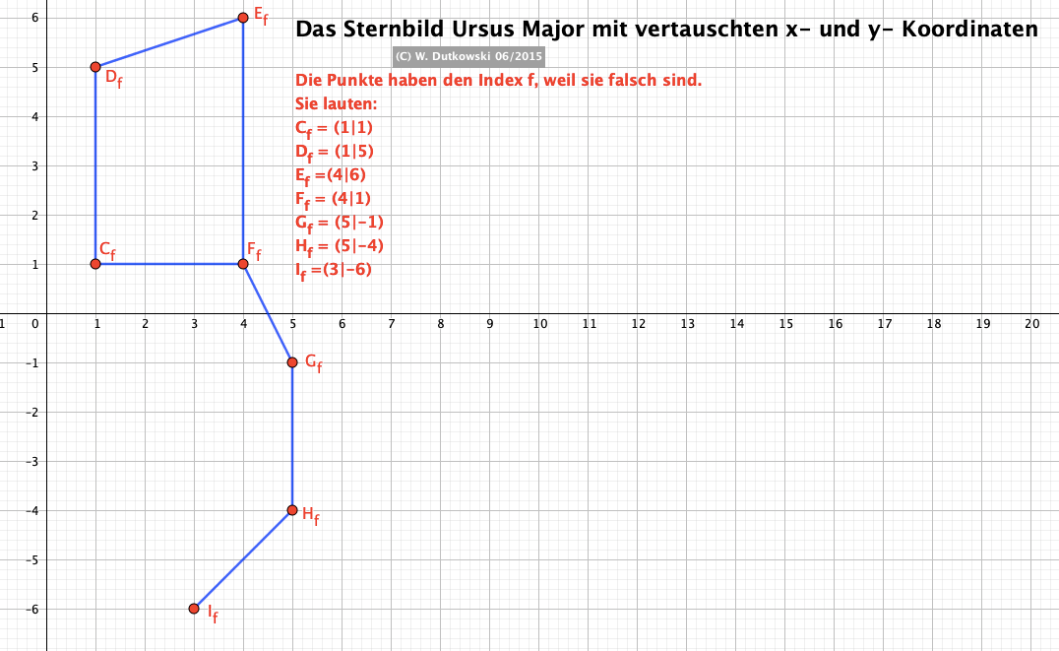
haben. Sie dürfen also x und y niemals vertauschen. Das nachfolgende Applet zeigt Ihnen, was passiert, wenn Sie diese Regel nicht beachten.Koordinatenspiel
Lösungsbild