E04 vajon 64 ≟ 65
Egy hamis(?) bizonyítás
Matematikai tanulmányaink során bizonyára többen találkoztak ezzel a bőséges hivatkozással rendelkező feladvánnyal.
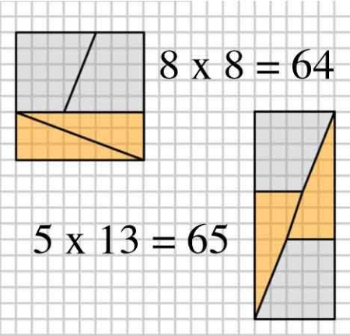
Ezt a kérdést járjuk kicsit körbe az alábbi GeoGebra alkalmazás segítségével.
Feladat:
- Osszunk fel egy négyzetet az alábbi módon két derékszögű trapézra és két derékszögű háromszögre, majd a kapott alakzatot rendezzük át úgy, hogy a négyzetből kapott síkidomok téglalapot alkossanak.
Néhány kérdés:
- Alaphelyzetben 5:3 arányban osztottuk fel a 3+5 = 8 egységnyi négyzetet, így látható (??), hogy az 1 területű paralelogrammával nagyobb a téglalap a négyzetnél.
- Vajon hogyan változik a rajz és a síkidomok területe, ha ezt az arányt (a ▶ gombbal) rendre 8:5, 13:8 ... vagy lefelé haladva (a ◀ gombbal) 3:2 , 2:1 arányban változtatjuk?
- Miként módosul a feladat, ha a felosztás b:a arányát a tetszőlegesen választható a, b (egész) számokkal adjuk meg, majd ugyancsak a ◀ ▶) gombokkal változtatjuk?
- Hogyan tudnánk a kapott sejtést igazolni?
- Ha a és b egész szám, akkor a téglalap és négyzet területének a különbsége milyen egész szám lehet (és milyen nem)?
- Milyen arányban kellene felosztanunk a négyzetet ahhoz, hogy az átrendezés helyes legyen?