PC: 1st Day on Inverse Trig. Functions
Investigating Inverses
Recall that, for any relation, the graph of this relation's inverse can be formed by reflecting the graph of this relation about the line y = x (Identity Function).
Recall that all functions are relations, but not all relations are functions.
In the applet below, you can input any function f and restrict its natural domain, if you choose, to input (x) values between -10 and 10. You also have the option to graph the function over its natural domain.
Answer the next three questions then Interact with this applet for a few minutes, then complete the activity questions that follow.
Functions and one to one functions?
What causes a relation to be a function and what causes a function to be a one to one function? Explain.
Determining if a relation is a function?
What test do we use to determine a relationship is a function graphically?
Determining if a relation is a one to one function?
What test do we use to determine an inverse of a relationship will be a function graphically?
Investigating Inverses
Directions:
Directions:
1) Choose the "Default to Natural Domain of f" option.
2) Enter in the original function.
3) Choose "Show Inverse Relation". 4) Is the graph of this inverse relation the graph of a function? Explain why or why not.
5) If your answer to (4) above was "no", uncheck the "Default to Natural Domain of f" checkbox.
6) Now, can you come up with a set of Xmin and Xmax values so that the function shown has an inverse
that is a function? Explain.
Repeat steps (1) - (6) again, this time for different functions f that are in our library.
I. A linear function
II. A cubic function
III. A rational function
IV. A trigonometric function
etc.
Notation for Trigonometric Inverse Functions (Notice the two different versions for Inverses).

Watch the video to understand how to move both red and black dots.
Finding the domain restrict for the inverse of Sine function. For the function y = cos(x), move the xMin and xMax to restrict the domain of this original function. Is it possible to restrict the domain so the inverse relation (with dashed graph) becomes
Function?
Why is the graph of y = sin(x) a function? Explain. Be sure to use the terms "input" and "output" in your explanation.
Pay attention to the quadrant inverse sine is restricted to.
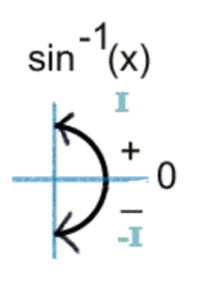
Restricted range for inverse sine? Hint: The angle can only be in quadrant I or IV.
Finding the domain restrict for the inverse of Cosine function. For the function y = cos(x), move the xMin and xMax to restrict the domain of this original function. Is it possible to restrict the domain so the inverse relation (with dashed graph) become
Function?
Why is the graph of y = cos(x) a function? Explain. Be sure to use the terms "input" and "output" in your explanation.
Pay attention to the quadrant inverse sine is restricted to.
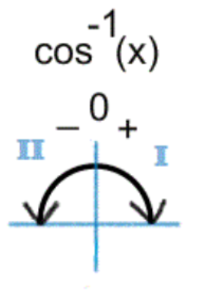
Restricted range for inverse cosine? Hint: The angle can only be in quadrant I or II.
Click the animate button and watch the trace of the inverse function of tangent. Pay attention to the range of the inverse function.
Range of the inverse tangent function.
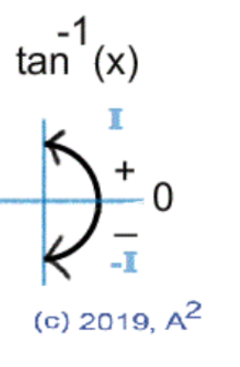
Range of the inverse tangent function? Angles?
Watch the video first
Evaluate the expression below. Be sure to enter an exact value! If you'd like, feel free to reposition the triangle and label its sides to help you solve this problem.
Practice Solving Two Step Linear Equations. Give it a try.
Solving simple trigonometric equations. Use your unit circle when appropriate or use your calculator (your calculator will only give you one solution).
Feedback
What did you like about this activity?
What did you not like about this activity?