Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Interpreting a Visualization of a Point and Estimate of a Population Mean for Small Samples (t-distribution)

Author:Annauen Joy Abellana Empaces

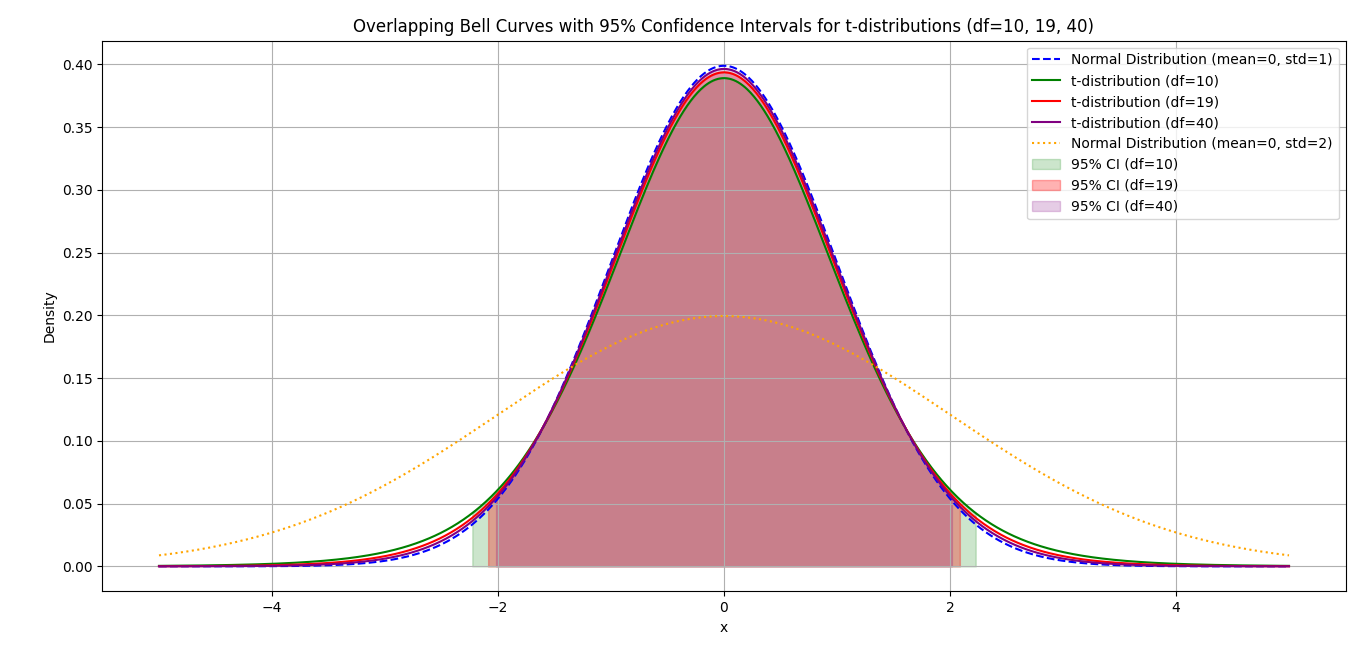
Overlapping Bell Curves with Confidence Intervals for t-distribution (df=19)

Overlapping Bell Curves with Confidence Intervals for t-distribution (df=19)
Interpreting the Image: Understanding t-Distribution vs. Normal Distribution In this image, we are comparing the t-distribution with the normal distribution, focusing on how the two curves behave under different conditions. First, we can observe that the t-distribution curve is lower and wider than the normal distribution curve. This is a key characteristic of the t-distribution, which tends to have heavier tails. The t-distribution is used when dealing with small sample sizes, and its shape reflects the additional variability inherent in smaller samples. As we increase the sample size, the degree of freedom (df) also increases, and we see that the t-distribution curve becomes more similar to the normal distribution. This happens because with larger sample sizes, the sample mean becomes a more accurate estimate of the population mean, reducing the variability, and making the t-distribution approach the normal distribution. At a 95% confidence level, we observe that as the degree of freedom increases, the confidence interval for the population mean becomes wider. This is because, for smaller sample sizes (lower df), there is more variability in the sample means, leading to a larger spread in the estimated population means. As the sample size (and df) increases, the variability decreases, and the confidence interval becomes narrower, making the estimate more precise. In summary, the image illustrates that:
  • The t-distribution is wider and lower compared to the normal distribution, especially with small sample sizes.
  • As the sample size and degree of freedom increase, the t-distribution curve approximates the normal distribution.
  • A lower degree of freedom (df) leads to a larger region for population mean estimates at a 95% confidence level, reflecting how small sample sizes increase variability in the sampling distribution.

Comparing a t-distribution and a normal distribution

What is the primary difference between a t-distribution and a normal distribution?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

t-distribution have heavier tails than the normal distribution

Why does the t-distribution have heavier tails than the normal distribution?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Sample size increase and the shape of the t-distribution

As the sample size increases, what happens to the shape of the t-distribution?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

95% confidence interval

What does a 95% confidence interval represent?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

(df) and the t-distribution

How does the degree of freedom (df) affect the t-distribution?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Sample size increase and the confidence interval

What happens to the confidence interval when the sample size increases?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Lower degree of freedom (df)

What effect does a lower degree of freedom (df) have on the confidence interval for the population mean at a 95% confidence level?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Sample Python Script to recreate this output

import numpy as np import matplotlib.pyplot as plt from scipy.stats import t, norm x = np.linspace(-5, 5, 1000) normal_curve = norm.pdf(x, 0, 1) t_curve_19 = t.pdf(x, 19) t_curve_10 = t.pdf(x, 10) t_curve_25 = t.pdf(x, 25) normal_curve_2 = norm.pdf(x, 0, 2) CI_95 = 0.95 CI_90 = 0.90 CI_99 = 0.99 t_critical_90_19 = t.ppf(1 - (1 - CI_90) / 2, df=19) t_critical_95_19 = t.ppf(1 - (1 - CI_95) / 2, df=19) t_critical_99_19 = t.ppf(1 - (1 - CI_99) / 2, df=19) plt.figure(figsize=(10, 6)) plt.plot(x, normal_curve, label='Normal Distribution (mean=0, std=1)', color='blue', linestyle='--') plt.plot(x, t_curve_19, label='t-distribution (df=19)', color='red') plt.plot(x, normal_curve_2, label='Normal Distribution (mean=0, std=2)', color='green', linestyle=':') plt.fill_between(x, 0, t_curve_19, where=(x >= -t_critical_90_19) & (x <= t_critical_90_19), color='red', alpha=0.2, label='90% CI (df=19)') plt.fill_between(x, 0, t_curve_19, where=(x >= -t_critical_95_19) & (x <= t_critical_95_19), color='red', alpha=0.3, label='95% CI (df=19)') plt.fill_between(x, 0, t_curve_19, where=(x >= -t_critical_99_19) & (x <= t_critical_99_19), color='red', alpha=0.4, label='99% CI (df=19)') plt.title('Overlapping Bell Curves with Confidence Intervals for t-distribution (df=19)') plt.text(0.5, 1.0, 'Overlapping Bell Curves with Confidence Intervals for t-distribution (df=19)', ha='center', va='top') plt.xlabel('x') plt.text(0.5, 0, 'x') plt.ylabel('Density') plt.text(0, 0.5, 'Density') plt.legend() plt.grid(True) plt.tight_layout() plt.show() t_curve_10 = t.pdf(x, 10) t_curve_19 = t.pdf(x, 19) t_curve_40 = t.pdf(x, 40) normal_curve_2 = norm.pdf(x, 0, 2) CI_95 = 0.95 t_critical_95_10 = t.ppf(1 - (1 - CI_95) / 2, df=10) t_critical_95_19 = t.ppf(1 - (1 - CI_95) / 2, df=19) t_critical_95_40 = t.ppf(1 - (1 - CI_95) / 2, df=40) plt.figure(figsize=(10, 6)) plt.plot(x, normal_curve, label='Normal Distribution (mean=0, std=1)', color='blue', linestyle='--') plt.plot(x, t_curve_10, label='t-distribution (df=10)', color='green') plt.plot(x, t_curve_19, label='t-distribution (df=19)', color='red') plt.plot(x, t_curve_40, label='t-distribution (df=40)', color='purple') plt.plot(x, normal_curve_2, label='Normal Distribution (mean=0, std=2)', color='orange', linestyle=':') plt.fill_between(x, 0, t_curve_10, where=(x >= -t_critical_95_10) & (x <= t_critical_95_10), color='green', alpha=0.2, label='95% CI (df=10)') plt.fill_between(x, 0, t_curve_19, where=(x >= -t_critical_95_19) & (x <= t_critical_95_19), color='red', alpha=0.3, label='95% CI (df=19)') plt.fill_between(x, 0, t_curve_40, where=(x >= -t_critical_95_40) & (x <= t_critical_95_40), color='purple', alpha=0.2, label='95% CI (df=40)') plt.title('Overlapping Bell Curves with 95% Confidence Intervals for t-distributions (df=10, 19, 40)') plt.text(0.5, 1.0, 'Overlapping Bell Curves with 95% Confidence Intervals for t-distributions (df=10, 19, 40)') plt.xlabel('x') plt.text(0.5, 0, 'x', ha='center', va='bottom') plt.ylabel('Density') plt.text(0, 0.5, 'Density') plt.legend() plt.grid(True) plt.tight_layout() plt.show()

Additional Tangible Experience for this Lesson

Additional Notes:
  1. Prerequisites for Running the Script: Ensure that you:
    • Have Python installed (preferably version 3.7 or higher).
    • Have pip installed for managing Python packages.
  2. Virtual Environment (Optional): It’s a good practice to create a virtual environment for your project to avoid package conflicts. Here’s how you can do it:
python -m venv myenv source myenv/bin/activate # On Linux/Mac myenv\Scripts\activate # On Windows pip install numpy matplotlib scipy Example: Please save the script as a .py file and save it to your desktop. Step 1. At your terminal (just type "cmd" in the search box of your OS): Step 2. Run the script by following this command template: python "C:\Users\<Your Name>\Desktop\<Folder Name>\<Script Filename>" Example: python "C:\Users\Annauen Joy Ravacio\Desktop\PYTHON SCRIPTS\Small Sample t-curve.py" Have fun! Thank you for your kind support.

New Resources

Discover Resources

Discover Topics