9. The Topos of Music
Esta actividad pertenece al libro de GeoGebra Música y Matemáticas.
TOPOLOGÍA MUSICAL (2ª parte)
Publicado en la sección Música y matemáticas de Divulgamat
Septiembre 2009
Mazzola
En 1989 el matemático suizo Guerino Mazzola publica "Geometría del Tono" que aplica los grupos de isometría, la teoría de Galois sobre conceptos -en vez de sobre polinomios algebraicos- y el álgebra categórica al análisis musical.

Topos
En 2002, Mazzola publica una profunda y mejorada ampliación de ese trabajo, bajo el título “The Topos of Music”. Este título tiene doble sentido. Por una parte, se puede traducir de forma general como “El lugar de la música”. Pero admite otro sentido mucho más concreto. Los “Topos” son objetos matemáticos (un tipo particular de Categoría) que vienen a reflejar las posibles visiones o perspectivas de un lugar abstracto a partir de las propiedades o relaciones matemáticas necesarias para su coherencia lógica.
Intuitivamente, en la Teoría de Categorías se usan flechas en vez de puntos, es decir, los objetos no son entes estáticos, sino el cúmulo de todas las posibles visiones o perspectivas en un lugar (topos) dado. Dicho de otra forma, se priman “las relaciones entre los objetos individuales” que conserven la estructura, más que los propios objetos en sí.
The Topos of Music
En esta obra de Mazzola se puede observar el gran progreso de las Matemáticas, la Teoría de la Música y el desarrollo de las Nuevas Tecnologías en la última década del siglo XX.

Mazzola crea una base, basada en los fundamentos teóricos de los Topos, que permite establecer relaciones lógicas y geométricas entre los objetos básicos de la Teoría Musical. Esta base incluye el análisis del ritmo, la melodía y la armonía.
A partir de esa base teórica, Mazzola puede establecer topologías y clasificaciones de los objetos musicales, analizando sus relaciones dentro de ese Topos. Un punto clave en esas relaciones, como no podía ser de otro modo, reside en la presencia de la periodicidad como uno de los fundamentos musicales. La aritmética modular tiene un importante papel en muchas de las relaciones rítmicas, melódicas y armónicas.
Dado el amplio abanico de recursos matemáticos necesarios para establecer el Topos que permita el estudio de los objetos musicales, en la propia obra se incorporan anexos sobre las teorías de Conjuntos, Correspondencias, Monoides, Grupos, Anillos, Álgebras, Módulos, Transformaciones lineales y afines, Cálculo, Geometría y Topología algebraica, Categorías, Topos y Lógica.
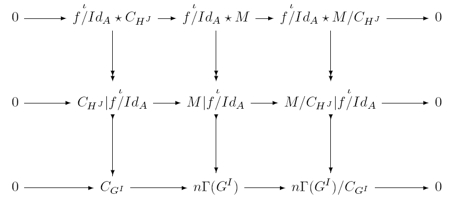
Igualmente, otro anexo recoge los fundamentos de la naturaleza y análisis del Sonido y nuestra Percepción del mismo, mostrando especial interés por los modelos de consonancia y la disonancia.
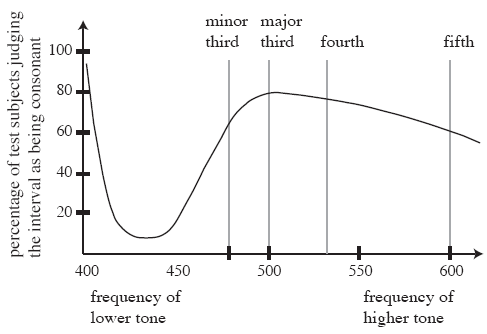
Intentar sintetizar aquí esta extensa obra de Mazzola es inviable. La publicación cuenta con más de 1300 páginas cuajadas de densa información, además de un CD con ejemplos del uso de programas informáticos creados específicamente para el análisis musical. Nos limitaremos a describir brevemente algunas de las imágenes que ilustran The Topos of Music, con la esperanza de que tal vez, casi por sí mismas, comuniquen algunas de las líneas de investigación que allí
aparecen.