5.1 Distância entre ponto e plano
Introdução
O objetivo dessa seção é demonstrar como é feito o calculo para distância entre um ponto e um plano no espaço. Chamaremos o plano de 
e o ponto genérico de A. A distância entre esses dois elementos pode ser denotada também como D(,A), lembrando que quando nos referimos à distância sempre quer dizer a menor distância entre eles.
e o ponto genérico de A. A distância entre esses dois elementos pode ser denotada também como D(,A), lembrando que quando nos referimos à distância sempre quer dizer a menor distância entre eles.Desenvolvimento
Para começar é bom lembrar de alguns detalhes importantes:
1º detalhe importante: a equação cartesiana do plano é dada na forma 
.
Importante: os coeficientes "a","b" e "c" são as coordenadas de um vetor normal ao plano (normal é o mesmo que perpendicular).
Exemplo: se o plano é descrito como x-y+2z=0, o vetor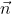 
=(1,-1,2) é um vetor normal à esse plano.
2º detalhe importante: esse vetor normal ao plano (que aparece na equação) pode ser escrito como produto vetorial de 
, sendo 
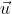e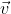 
dois vetores quaisquer que são paralelos ao plano (de maneira informal e de fácil compreensão imagine dois vetores quaisquer que estão "contidos" no plano, esses serão os vetores 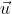e .
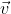importante: os valores d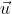e e 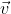não importam, porque eles só irão aparecer para finalidade de dedução, na prática você não usará eles)
Observe a situação no espaço para melhor visualização:
Vermelho- Vetor normal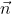
Verde limão- Vetor
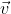Laranja - Vetor
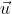Ponto A- representado pelo ponto azul
Olhando para essa disposição, é possível se recordar que é parecida com o que foi feito na seção passada(distância entre retas no espaço). Para relembrar, foi construído um prisma (pelo produto misto de três vetores) e dali tiramos a distância.
Porém, para poder usar tal estratégia ainda falta um vetor, que será crucial para esse estudo.
Considere um ponto qualquer Q que pertence ao plano e analise o vetor preto 
. (é importante frisar que VOCÊ é quem escolhe o ponto Q, ele só precisa pertencer ao plano )
e analise o vetor preto )Agora sim, podemos adotar a estratégia da seção anterior de comparar o prisma formado pelos vetores 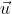, 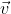e . Lembrando que 
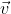(produto vetorial de e ).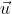
Assim, temos como calcular o Volume do prisma de duas maneiras: Volume pelo produto misto dos três vetores e o Volume pela definição algébrica de prisma (que é Área da base * Altura).
Importante! A altura que comentamos aqui é a distância entre o ponto e o plano.
Como as duas maneiras de calcular o volume são equivalentes, pois se tratam do mesmo prisma, temos como relacionar ambos.
Por produto misto:
Volume=
Por definição:
Volume=Área da base * Altura
Lembre que a área da base é o módulo do produto vetorial de 
Logo, Volume= * Altura
Como ambos os volumes são iguais, temos que:
=* Altura
Altura = 
Sabemos que .
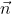é o Vetor normal(perpendicular) ao plano.
Então finalmente, temos que:
Altura=D(,A)=
,A)=