Σταθερή υποτείνουσα - μέγιστο ορθογώνιο
Οδηγίες
Στη δραστηριότητα που ακολουθεί εξετάζουμε το πρόβλημα:
"Από όλα τα ορθογώνια τρίγωνα με σταθερή υποτείνουσα α, ποιο έχει το μέγιστο εμβαδόν" με γεωμετρική διατύπωση ή "από όλους τους θετικούς πραγματικούς αριθμούς με σταθερό άθροισμα τετραγώνων, ποιοι έχουν το μέγιστο γινόμενο" με αλγεβρική διατύπωση .
- Στο 1ο παράθυρο, εμφανίζεται το ορθογώνιο τρίγωνο ΑΒΓ με κάθετες πλευρές β και γ, ένας δρομέας α που ορίζει το μήκος της υποτείνουσας και ένα ορθογώνιο με πλευρές β και γ.
- Στο 2ο παράθυρο, εμφανίζεται ένα σημείο Ρ με συντεταγμένες (γ, βγ)
Πειραματισμός
Αρχικά διατυπώστε συμβολικά το πρόβλημα με χρήση των πλευρών α,β και γ.
- Τί εκφράζει το γινόμενο για το ορθογώνιο τρίγωνο ΑΒΓ και το ορθογώνιο τ;
- Από τη μορφή της καμπύλης του σημείου Ρ, μπορείτε να εικάσετε αν και πότε το γινόμενο λαμβάνει μέγιστη τιμή;
- Πατήστε το κουμπί "max" για να συγκρίνετε τα ευρήματά σας.
- Τί φαίνεται να ισχύει τότε για το ορθογώνιο τ;
- Ποια εικασία μπορούμε να διατυπώσουμε σχετικά με το αρχικό μας ερώτημα;
Σύνταξη Απόδειξης
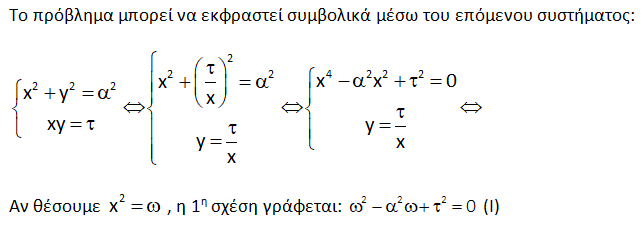
Ανοίξτε το διακόπτη "1η αναπαράσταση". Εμφανίζεται η γραφική παράσταση του τριωνύμου
- Σύρετε το σημείο Β σε διάφορες θέσεις.
- Τί παρατηρείτε για τις σχετικές θέσεις της παραβολής q με τον άξονα xx΄ ;
- Αξιοποιήστε το συμπέρασμα που προκύπτει από την προηγούμενη παρατήρηση για να συντάξετε την απόδειξη της εικασίας σας.
Αλγεβρική Απόδειξη

Γεωμετρική Απόδειξη
Ανοίξτε το διακόπτη «2η Αναπαράσταση».
Εμφανίζεται το ημικύκλιο διαμέτρου ΒΓ και το (επίσης) εγγεγραμμένο ορθογώνιο τρίγωνο ΒΛΓ εντός αυτού, όπου ΛΜ είναι μεσοκάθετος της ΒΓ και το ΑΝ ύψος του τριγώνου ΑΒΓ. Σύρετε το σημείο Β σε διάφορες θέσεις.
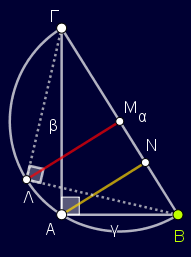
- Τί παρατηρείτε για τη σχέση των τμημάτων ΑΝ και ΛΜ;
- Χρησιμοποιώντας ως γνωστή τη σχέση που ισχύει σε κάθε ορθογώνιο τρίγωνο: να αξιοποιήσετε αυτά τα στοιχεία για την απόδειξη της εικασίας σας.
Απόδειξη

Επέκταση δραστηριότητας
1. Η γραμμή που διαγράφει το σημείο Ρ(γ,βγ), "φαίνεται" να ομοιάζει με παραβολή. Μπορείτε να ελέγξετε αν πρόκειται πράγματι για παραβολή;
(Θα χρειαστεί να βρείτε τον τύπο της συνάρτησης που περιγράφει τη συμμεταβολή της μεταβλητής τ=βγ συναρτήσει της πλευράς γ)
Απάντηση
