Arithmetische Friesmuster - Teil 2
Aufgabe 6
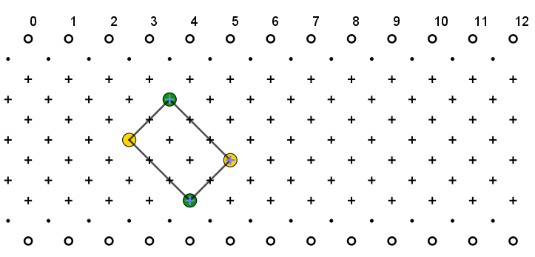Das obige Bild symbolisiert ein ausgefülltes arithmetisches Fries. Das Zeichen O steht für eine 0, der kleine Punkt in der zweiten und vorletzten Zeile für eine 1. Die Pluszeichen in den übrigen Zeilen stehen für beliebige positive Zahlen. Die Nummern am oberen Rand benötigen wir später.
Das "Quartett", aus dem der Ausdruck ad - bc bei der unimodularen Gleichung gebildet wird, soll nun variiert werden: Statt unmittelbar benachbarter Zahlen sollen nun die Ecken eines "Diagonalenrechtecks" wie im Bild benutzt werden, wobei stets "gelb mal gelb minus grün mal grün" bzw. "links mal rechts minus oben mal unten" gerechnet werden soll. Wir nennen das "das Quartett berechnen". Im Bild unten ergibt sich z.B. 313 - 22 = 35.
a) Führe diese Rechnungen am ausgefüllten Fries aus Aufgabe 4 (Bild unten) an mehreren Stellen durch. (Du kannst dazu in das Applet schreiben oder zeichnen.) Kannst du eine Gesetzmäßigkeit entdecken? Wenn nicht: Sieh dir zunächst Tipp 1 an!
b) Beschreibe deine Beobachtungen zu a).
c) Kombiniere jetzt die in a), b) durchgeführten Schritte und versuche, eine Vermutung für eine allgemeine "Quartettregel" zu formulieren. Wenn du nicht weiterkommst, überlege, welche Rolle die beiden Karos in Tipp 2 spielen könnten.
d) Überprüfe, ob und wie sich die unimodulare Gleichung und die in b) betrachteten Fälle als Sonderfälle der vermuteten Quartettregel erweisen.
e) Leite die Beobachtung aus Aufgabe 4b) aus der Quartettregel her. Du kannst dazu das Applet mit den verschiebbaren Diagonalen benutzen. Erläutere dein Vorgehen im Antwortfenster. Begründe damit, dass das Friesmuster aus Aufgabe 4 eine Gleitspiegelsymmetrie bezüglich der Mittellinie hat und periodisch ist mit der Periodenlänge 10 (Diagonalen). Formuliere eine entsprechende Aussage für beliebige arithmetische Friesmuster. Wie bestimmt man die Periodenlänge?
f) Untersuche, unter welcher Bedingung das Friesmuster zusätzlich punktsymmetrisch ist.
g) Untersuche, unter welcher Bedingung das Fries nur ganze Zahlen enthält.
Aufgabe 7
a) Formuliere die unimodulare Gleichung und die vermutete Quartettregel aus Aufgabe 6 in dieser Schreibweise.
b) Drücke die Gleitspiegelung und die Periodizität (vgl. Aufgabe 6d) in der neuen Schreibweise aus.
c) Zeige mit Hilfe der Quartettregel, wie man die Zahl im rosa markierten Feld direkt (ohne Zwischenschritte) aus den Zahlen der beiden grau unterlegten Diagonalen berechnen kann.
Beschreibe das Verfahren allgemein.
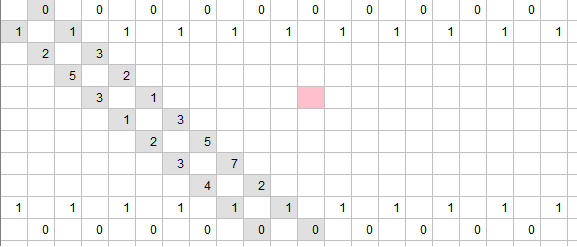
d) Begründe, warum man das Verfahren in c) nicht für beliebig weit rechts liegende Elemente anwenden kann. Überlege und begründe, wie man das Fries nach unten (und oben) erweitern müsste, damit die Quartettregel für beliebig weit entfernte Diagonalen erhalten bleibt.
Beweisidee für die Quartettregel
Aufgabe 8
a) Führe die obigen Ideen ausführlich aus. b) Zeige, dass die allgemeine Definition von (x,y) mit den Vorgaben für (0,y) und (1,y) sowie mit der Begrenzung durch Nullzeilen (Zeile 0 und n) und Einszeilen (Zeile 1 und n-1) verträglich ist. c) Beweise die Quartettregel.