Aire d'un octogone et d'un disque
Source GeoGebra
Enoncé
Dans le cadre des calculs d'aire, de l'aire d'un disque cet exercice peut être utilisé soit comme introduction, soit comme prolongement.
Suggestion pédagogique :
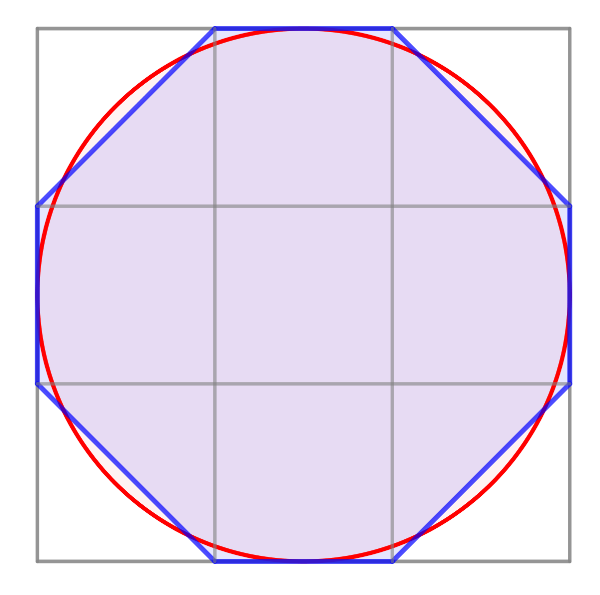
1) montrer la figure aux élèves et leur demander ce que cela leur inspire comme question mathématique. On en vient à se demander laquelle des deux aires, celle de l'octogone ou du disque est la plus grande
- Sachant que les 9 carrés gris ont pour côté 2cm, comparer l'aire du disque rouge et celle de l'octogone bleu.
Ou bien :
2) Déterminer une valeur approchée de Pi en utilisant cette figure.
Si le théorème de Pythagore a déjà été vu, on pourra comparer les approximations obtenues avec le cacul des périmètres et celui des aires. Celui des aires donne une fraction d'entiers ce qui amène à parler de l’irrationalité de pi.
Point historique
Dans le papyrus Rhind (rédigé vers 1650 av. J.-C.) Ahmes suggère une quadrature du disque (problème 48).
Comparaison de la superficie d'un disque de diamètre 9 à celle de son carré circonscrit, dont la taille d'un côté est également de 9. Ratio de la superficie du disque au carré?La réponse donnée est 64/81. Cela revient à dire que l'aire d'un disque de diamètre 9 est égale à celle d'un carré de côté 8. Cette approximation de la quadrature du cercle permit aux Égyptiens de se passer de la constante π en la utilisant que le rapport de l'aire du disque au carré qui le circonscrit est 64/81. On ne sait pas comment ils ont pu trouver ce rapport de 64/81 mais certains auteurs comme Petr Beckmann (A History of Pi) pensent qu'ils ont pu utiliser cette figure étudiée ici qui amène au rapport 63/81 si on prend des petits carrés de côtés 3. Or 63 est proche de 64 qui est le carré de 8. cf problèmes 41-43-48-50 du papyrus. wikipedia.org/wiki/Papyrus_Rhind