Bestimmung der Steigung einer Geraden
Nachdem wir herausgefunden haben wie sich der Parameter der proportionalen Funktion auf die Steigung der Geraden auswirkt, stellt sich die Frage, wie man die Steigung einer Geraden bestimmen kann.
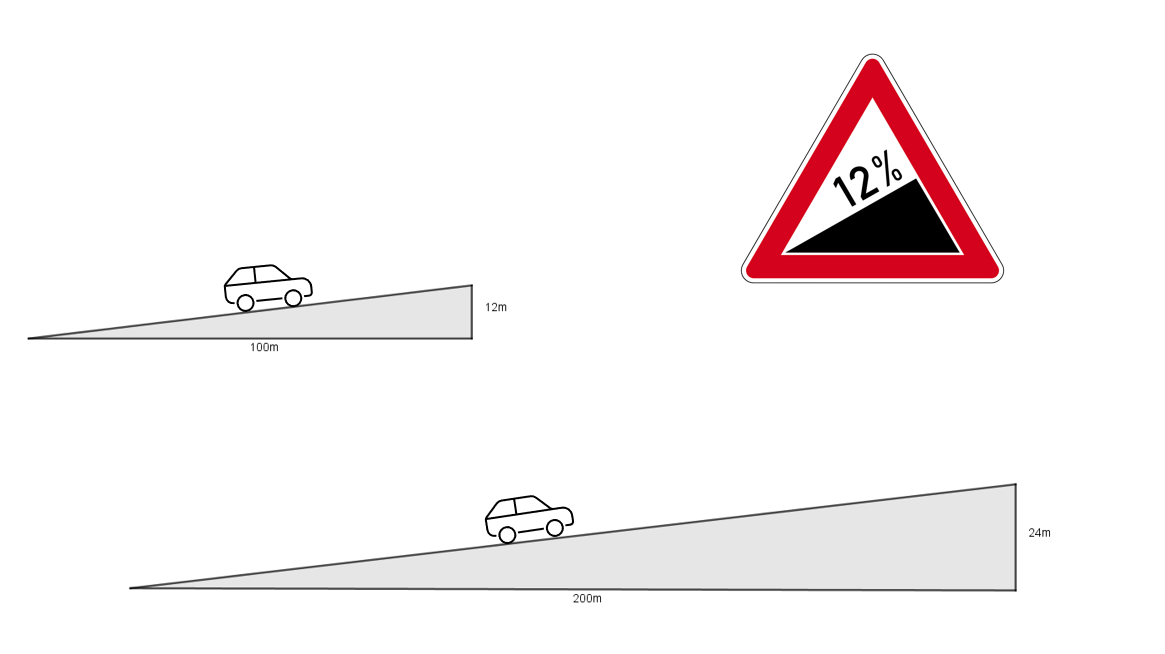
Aufgabe 1: Die Steigung spielt auch im Straßenverkehr, wenn die Straße bergauf oder bergab verläuft, eine große Rolle. An solchen Stellen gibt es Straßenschilder, die die Steigung der Straße in Prozent angeben.
Betrachte das Beispiel unten. An beiden Straßen steht das gleiche abgebildete Straßenschild.
Stelle eine Vermutung auf, wie man die Steigung berechnen kann.
Die Steigung von Geraden bestimmt man ähnlich zu der Steigung von Straßen über ein sogenanntes Steigungsdreieck, welches du nun kennenlernen wirst.
Im Koordinatensystem unten ist der Graph einer proportionalen Funktion umgebildet.
Aufgabe 2a) Bewege die Punkte P und Q auf der Geraden. Beobachte den Quotienten mit dem sich die Steigung berechnet. Notiere deine Beobachtungen.
Aufgabe 2b) Variere die Steigung der Geraden. Wähle dabei auch negative Steigungen. Notiere deine Beobachtungen.
Aufgabe 2c) Variere nun erneut die Steigung der Geraden und bewege zudem die Punkte P und Q.
Gibt es Positionen von P und Q für die man den Quotienten besonders gut berechnen kann?
Stelle eine Vermutung auf, wie sich und mit Hilfe der Punkte P und Q berechnen lassen.
Aufgabe 3: Kreuze alle Aussagen an, die wahr sind.
Aufgabe 4: Vervollständige den folgenden Lückentext und übertrage diesen anschließend als Merksatz in dein Heft. Übertrage ebenfalls das Beispiel in dein Heft.
![[size=50]Quelle: https://unterrichten.zum.de/wiki/Lineare_Funktionen/Station_2[/size]](https://www.geogebra.org/resource/tre96m93/pHJmgs3jqUyG0Tcs/material-tre96m93.png)
Wenn du dir noch etwas unsicher bist, wie man die Steigung einer Geraden bestimmt, schaue dir folgendes Video an: