完全グラフをKnで作る
1.完全グラフ
このワークシートはMath by Codeの一部です。
グラフは頂点の集合Vと辺の集合Eからなる。G=（V,E)とかくことがある。
逆に、V（G）、E（G)のように、Gを主体にかくこともある。
形はどうであれ、VもEもGと一致しているグラフFをGと同型(isomorphic)グラフというね。
VもEもGもGの部分集合になっているグラフFをGの部分グラフ(subgraph)というのはわかるだろう。
特に、Vだけはそのまま全部含む部分グラフを全域部分グラフという。
Vはそのままで、Vの可能なすべての辺の集合をEPとすると、Eの補集合E＝EP-Eに切り替えた
グラフを補グラフという。
＜つながりを表す言葉＞
・２頂点ｐ，ｑをつなぐ辺eがあるとき、e={p,q}とかくことがある。
頂点ｐとｑはeで隣接して、辺eはｐとｑに接続しているという。
・２つの辺e、ｆをつなぐ点ｒがあるとき、
辺eとｆはｒで隣接してるという。
つまり、隣接は辺と辺または、頂点と頂点のように、同種のものが
となりあってつながっているときに使う。
接続は、種類に関係なく、辺と辺、頂点と頂点、頂点と辺がとなりあってつながっているときに使う。
・頂点V(G)の部分集合Uと、それらの要素にGで接続していたE(G)の部分FからなるグラフをUが誘導するグラフという。辺についても、部分集合が誘導するグラフ(induced subgraph)を考えることができるね。
・１つの点eがｋ個の辺の端にならば、点eの次数(degree)はｋだという。deg(e)=kとかく。
次数０の点を孤立点といい、次数１の点を端点というが、これは常識的なことば遣いだ。
maximum(各頂点の次数）＝最大次数、Δ（G）とかく。
minimum(各頂点の次数）＝最小次数、δ（G)とかく。
これも常識的なネーミングだね。
ただ、同じデルタを大文字小文字で区別しているのはわかりにくいかも。
・ｎ次の正則グラフはどの頂点の次数も等しくｎのグラフで、
特に、完全グラフ(complete graph) Kn＝(n,n-1)とは頂点数がｎでn-1次の正則グラフだ。
どの点からもn-1辺が出ているので、どの２つの頂点同士も隣接しているといえるね。
K1は１点グラフ。K2は線分。K3は正三角形と同型。K4は対角線のある正方形と同型。
K５は対角線のある正五角形と同型。
・グラフGに頂点や辺や頂点を足し引きしたグラフを考えることがある。
Gの１頂点をu、vとし、１辺をeとする。また、Gにない１頂点をw，１辺をuv={u,v}とする。
G-uは、uに接続するすべての辺を取り除いたグラフ。G-eは辺を１辺を消しただけのグラフだ。
G+wは、ｗだけなく、wとGを結ぶ辺を追加したグラフ。G+uvは辺１辺を足しただけのグラフだ。
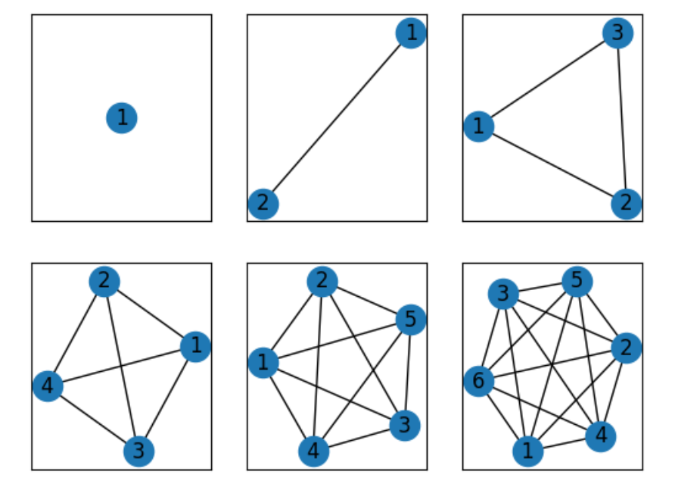
質問：完全グラフKnを順次書き出すコードはどうやって作りますか。
K1に辺がないのでこれは頂点(node)だけのグラフにする。
n=2からは、完全グラフを作って返す関数K(n）を作っておき、あとで順次使おう。
まず頂点リストVを作り、Vから２つ選んだ組み合わせとして辺の端点リストEをつくる。
そのあと、グラフのオブジェクトGを作ってから、GにEのデータを登録する。
表示のために、matplotlib.pyplotをpltに変名して、plt.subplot(行数、列数、通し番号）で
表示枠をかき、そのあとに中にGを毎回描けばよいね。
#[IN]Python
#========================================
import networkx as nx
import itertools
import matplotlib.pyplot as plt
n=6
G = nx.Graph()
G.add_node(1)
plt.subplot(2,3,1)
nx.draw_networkx(G)
def K(n):
V = list(range(1,n+1))
E = list(itertools.combinations(V,2))
G = nx.Graph()
G.add_edges_from(E)
return G
for i in range(2,n+1):
G=K(i)
plt.subplot(2,3,i)
nx.draw_networkx(G)
#========================================
[OUT]
完全グラフを生成しよう
２．グラフの加工
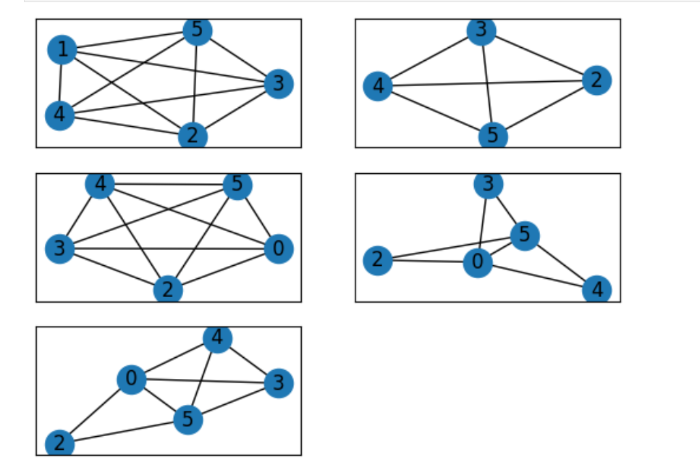
質問：グラフの要素のたしひき関数を作って、K５を加工するにはどうしますか？
頂点p追加はadd_node(p)
頂点p削除はremove_node(p)。辺には必ず端点があるので、１点を削除したら接続辺も削除される。
辺{p,q}追加はadd_edge(p,q)
辺{p,q}削除はremove_edge(p,q)
ただし、頂点削除は接続辺も連動して削除されるが、
頂点追加は孤立点が追加されるだけなので、既存の頂点と結ぶ辺のデータをGに追加する関数
add_node_with_edges(G,n)を作ってみよう。
#[IN]python
#=======================================================
import networkx as nx
import itertools
import matplotlib.pyplot as plt
def K(n):
V = list(range(1,n+1))
E = list(itertools.combinations(V,2))
G = nx.Graph()
for i in range(len(E)):
x,y = E[i][0], E[i][1]
G.add_edge(x,y)
return G
def add_node_with_edges(G,n):
V=G.nodes()
G.add_node(n)
for i in V:
G.add_edge(i,n)
return G
G=K(5)
plt.subplot(3,2,1)
nx.draw_networkx(G)
G.remove_node(1) #G-1
plt.subplot(3,2,2)
nx.draw_networkx(G)
add_node_with_edges(G,0) #G+0, G.add_node(0)では頂点だけが孤立点でたさせる
plt.subplot(3,2,3)
nx.draw_networkx(G)
G.remove_edge(2,3) #G-{2,3}
G.remove_edge(3,4) #G-{3,4}
G.remove_edge(2,4) #G-{2,4}
plt.subplot(3,2,4)
nx.draw_networkx(G)
G.add_edge(3,4) #G-{3,4}
plt.subplot(3,2,5)
nx.draw_networkx(G)
#=======================================================
[OUT]
グラフを加工しよう
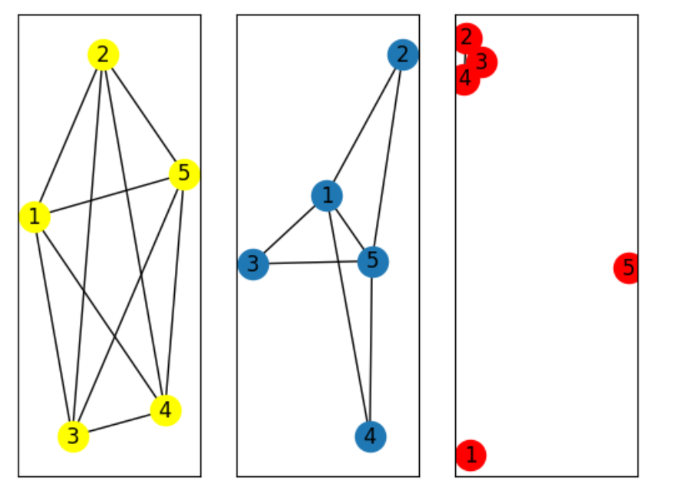
３．補グラフ
グラフの点が決まっているとき、完全グラフをかくことができた。
ということは、完全でないグラフとその補グラフをあわせると完全グラフになるのだから、
完全でないグラフは補グラフをかくことで、その特徴を裏側から炙り出せるでしょう。
質問：グラフからその補グラフを作るにはどうしたよいでしょうか。
グラフGの頂点Vから完全グラフの辺集合Eを作る。
そして、与えられたグラフの辺集合Fとの差集合Eh=E-Fを作る。
そして、G(V,Eh)で補グラフ作成関数comp(G)となるね。
#[IN]Python
#====================================================================
# 補グラフをかく。
import networkx as nx
import itertools
import matplotlib.pyplot as plt
def K(n):
V = list(range(1,n+1))
E = list(itertools.combinations(V,2))
G = nx.Graph()
G.add_edges_from(E)
return G
def comp(G):
V = G.nodes()
E = G.edges()
Kom = K(len(V))
F = Kom.edges()
Eh = list(set(F)-set(E))
H = nx.Graph()
H.add_nodes_from(V)
H.add_edges_from(Eh)
return H
G=K(5)
plt.subplot(1,3,1)
nx.draw_networkx(G,node_color='Yellow') #完全グラフ
G.remove_edge(2,3) #G-{2,3}
G.remove_edge(3,4) #G-{3,4}
G.remove_edge(2,4) #G-{2,4}
plt.subplot(1,3,2)
nx.draw_networkx(G) #不完全グラフ
H=comp(G)
plt.subplot(1,3,3)
nx.draw_networkx(H,node_color='Red') #補グラフ
#====================================================================
[OUT]
補グラフの辺は完全グラフの補集合
