Retas no Plano Cartesiano
Definição
Condição de alinhamento de três pontos no plano
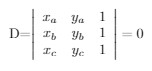
Verificando o alinhamento
Atividade 1
Movimente os botões na lateral direita. Cada um deles está associado a uma coordenada (x ou y) de um dos pontos (A, B ou C). Escolha uma posição para cada ponto e verifique o valor D. Esse valor é o resultado do determinante calculado conforme a explicação acima. Depois disso, clique na caixa de seleção "reta" e verifique se realmente os pontos estão alinhados ou não. Teste com várias coordenadas para cada ponto. Escolha uma posição deles e complete no espaço abaixo: Ponto A= Ponto B= Ponto C= Valor do determinante D= Resultado: Estão alinhados, sim ou não?
Inclinação da reta
Inclinação da reta
Atividade 2
Movimente o ponto A, movimentando assim a reta, e verifique o que acontece com o ângulo . O que representa esse ângulo?
Atividade 3
Movimento o ponto A, de modo que a reta fique perpendicular ao eixo OX. Qual é o valor de nessa situação?
Atividade 4
Aqui temos uma limitação na construção do applet pois, surge da definição que . Posicione o ponto A de uma forma que o ângula destacado apareça maior que 180º, escreva abaixo o ponto, o ângulo marcado no applet e determine a real inclinação da reta nessa situação.