Jednostavni račun smjese
Imamo dvije vrste robe: prve x kg po cijeni a kn i druge y kg po cijeni b kn i neka je a > b.
Trebamo dobiti smjesu čija će cijena biti s kn (b < s < a) za 1 kg.
Pitamo se : u kojem omjeru treba pomiješati navedenu robu?
Pomiješamo li robu, dobit ćemo ( x + y ) kg smjese po cijeni s kn.
Dakle:
slijedi:
što možemo pisati u obliku razmjera: x : y = ( s - b ) : (a - s )
Do tog omjera možemo doći pomoću sheme:
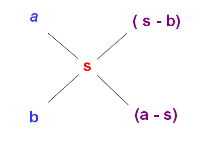
Primjer 1. Koliko litara vode treba pomiješati s 3 litre alkolhola jakosti 90%
ako želimo dobiti alkohol jakosti 60%?
Rj. U vodi nema alkohola, jakost vode je 0%.
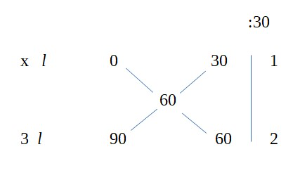
Pišemo: x : y = 1 : 2
(voda) x =
(alkohol) y =
Imamo y = 3 , uvrstimo: /:2,
Potrebno je uzeti 1.5 litara vode i pomiješati s 3 litre alkohola jakosti 90%
pa se dobije 4.5 litara alkohola jakosti 60%.
Primjer 2. Imamo dvije vrste bombona: od 59 kn i 44 kn (cijene za 1 kg).
Kako treba pomiješati bombone i koliko treba uzeti svake vrste ako želimo dobiti
20 kg bombona koji će se prodavati po 50 kn za 1 kg?
Rj.
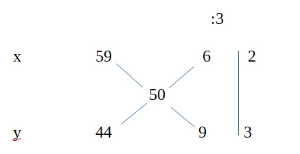
Omijer miješanja I. vrste (od 59 kn) i II. vrste (od 44 kn) bombona je
x : y = 2 : 3
I. vrsta (od 59 kn) x =
II. vrsta (od 44 kn) y =
Poznata je ukupna količina bombona: x + y = 20,
uvrstimo:
/:5
Izračunajmo: ,
Potrebno je pomiješati 8 kg bombona I. vrste (od 59 kn) sa 12 kg bombona II. vrste (od 44 kn).