Hihnan mitoittaminen
Koneen suunnittelussa hihnan mitoittaminen vaatii tarkkaa laskemista, missä tarvitaan
- Pythagoraan lausetta,
- kaaren pituuden laskemista,
- perustrigonometriaa sekä
- ympyräntangentin ymmärrystä.
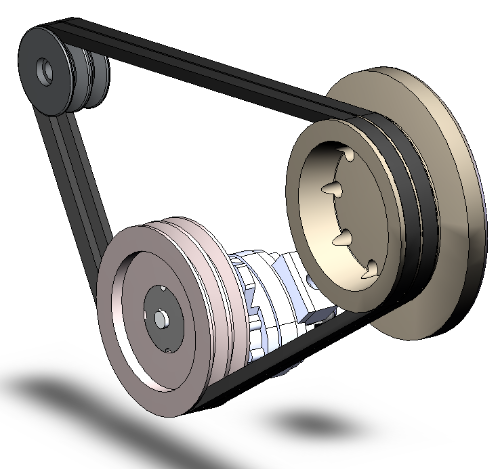
Yllä olevassa appletissa on hahmoteltu erään kolmen hihnapyörän kautta kulkevan hihnan mitoittamiseen tarvittavia laskuja. HUOM! Saat kuvaan lisää informaatiota klikkaamalla eri osia: mustaa ympyrän kehää ja suoria vihreitä osia.
Pienen hihnapyörän halkaisija on cm ja kahden muun cm. Keskipisteiden C ja E välinen etäisyys on 20 cm ja keskipisteiden E ja G välinen etäisyys myös 20 cm. Kulma CEG on suora. Määritetään vihreällä kuvatun hihnan pituus.
Hihnan suora osuus pisteestä K pisteeseen O on sama kuin keskipisteiden välinen etäisyys eli 20 cm.
Loput hihnan suorista osuuksista on helppo laskea Pythagoraan lauseen avulla. Kun suora osuus siirretään alkamaan pienen hihnäpyörän keskipisteestä, niin sitä vastaavan sivun pituus (senttimetriä).
Tällöin (cm).
Suoran osuuden NI määrittämiseksi on laskettava ensin janan CG pituus. Tämä saadaan suoraan Pythagoraan avulla annettuilla keskipisteiden välisillä etäisyyksillä eli
(cm), joten
(cm).
Hihnapyörien kautta kulkevan hihnan pituus saadaan sektorin kaaren pituuden kaavalla. Tätä varten on ensin määritettävä sektorin keskuskulman suuruus.
Kun hihnan suora osuus koskettaa hihnapyörää, niin hihnapyörän säteen ja suoran osuuden välille muodostuu suora kulma (suora osuus vastaa ympyrän tangenttia). Tämä kohta ei välttämättä ole 90 asteen kohdalla (vrt. piste J). Kulman määrittämiseksi voidaan käyttää samaa kolmiota kuin vastaavan suoran osuuden laskemiseksi. Kulma PCE on saman suuruinen kuin pisteen J ero 270 asteesta. Asiaa voi tarkastella vaikkapa suorakulmion CJLE avulla. Jos A4-arkki laitetaan pöydälle seinän viereen, niin seinän puoleista alakulmaa nostettaessa, seinän ja arkin väliin jäävä kulma on yhtä suuri kuin arkin ja pöydän väliin jäävä kulma. Sama tilanne on mainitussa suorakulmiossa.
Ylhäällä olevan hihnapyörän kulma on suora mutta kaari jatkuu vielä kulman verran. Kulma saadaan vähentämällä 180 asteesta ja .
Kolmio CQN on suorakulmainen, joten CN on sen hypotenuusa eli
Kolmiossa CGN voidaan hyödyntää kosinilausetta eli
Nyt
Täten sektorin kulma on
Pienen hihnapyörän kaaren kulman suuruus on siis
Alhaalla olevan hihnapyörän kaaren pituus on
Nyt pienen hihnaympyrän kaaren pituus on
(cm).
Ylhäällä olevan hihnapyörän kaaren pituus on
(cm).
Alhaalla olevan hihnapyörän kaaren pituus on
(cm).
Hihnan kokonaispituus on siis
cm.