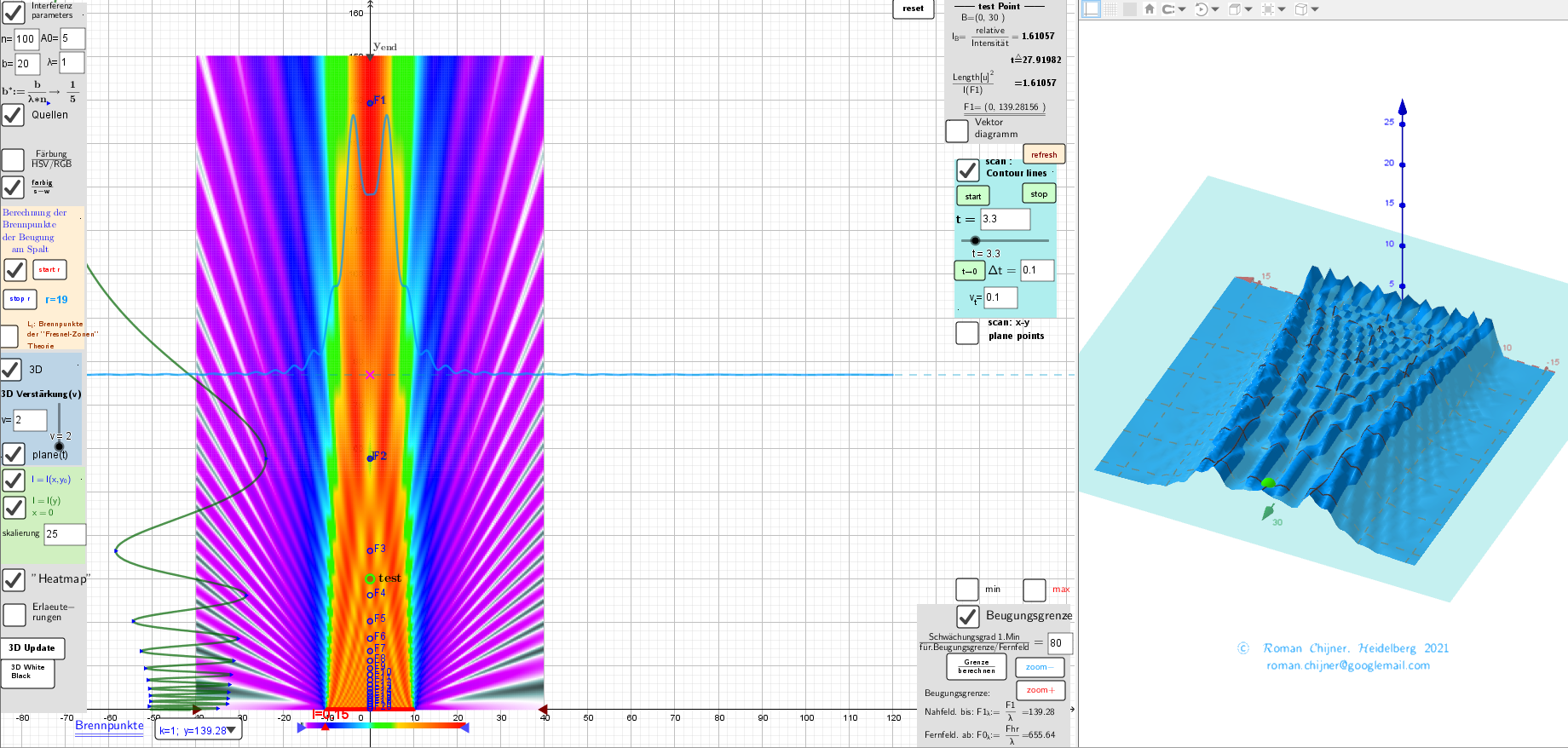
Multiple point source interference of damped waves and single slit diffraction: near, far field. Simulation./Überlagerung gedämpfter Wellen von vielen Punktquellen und Einzelspaltbeugung.
Räumliche Verteilung der Intensität der resultierenden Schwingung bei der Interferenz von (hier, n=100)-kreisförmigen Wellen(mit Dämpfung 1/sqrt(r)) der gleichen Amplitude und der gleichen Phase, die von einem eindimensionalen Array von Punktquellen emittiert werden. bλ=20- Spaltenbreite in Wellenlängeneinheiten. Fall bλ=6 wurde zuvor im Applet untersucht.
Hier ist eine Simulation, die die räumliche Verteilung der Intensität der resultierenden Schwingung berechnet. Eine Beschreibung des Programms finden Sie im Applet. Bilder des Beugungsmusters finden Sie im Applet.
Mit dem vorgeschlagenen Applet können Sie die Eigenschaften der entsprechenden 3D-Oberfläche der Schwingungsintensitätsverteilung auf der Wasseroberfläche untersuchen, indem Sie den Testpunkt entlang der Konturdiagrammzeichnung mit unterlegten Farben("Heatmap") verschieben.
*Aktivieren Sie das "3D"-Fenster, um die Beugungsfeldintensität sowie den entsprechenden Testpunkt auf dieser Fläche zu beobachten.
F1, F2,...F20 - "Brennpunkte" werden hier als extreme Intensitätspunkte auf der Spalte-Achse berechnet. Die Färbung erfolgt bei der Auswahl der maximalen Amplitude, die bei F1 ist. F0 dies ist der geschätzte Anfangspunkt des Gebiets der Fernfeld (Fraunhofer-Beugung). Es ergibt sich hier aus der Bedingung der Schwächung der Intensität im ersten Beugungsminimum des einzelnen Spalts im Vergleich zu seinem Wert im Bereich F1. Sie können "Schwächungsgrad 1.Min" im Applet ändern und die Änderungen untersuchen. Um die Intensitätsverteilung in diesem Bereich zu beobachten, muss eine andere Verstärkung für I=I(x, y0) eingestellt werden : skalierung=150.
Berechnungsformeln:
 Die Simulation mit Punktquellen erlaubt es, im Gegensatz zu Berechnungen, die mit Näherungsberechnungen des Beugungsintegrals verbunden sind, explizit die Kurven der Intensitätsverteilung des Beugungsfeldes sowie die 3D-Oberfläche der Intensitätsverteilung dieses Feldes zu erhalten.
Die Simulation mit Punktquellen erlaubt es, im Gegensatz zu Berechnungen, die mit Näherungsberechnungen des Beugungsintegrals verbunden sind, explizit die Kurven der Intensitätsverteilung des Beugungsfeldes sowie die 3D-Oberfläche der Intensitätsverteilung dieses Feldes zu erhalten.