Domino Effect
This activity belongs to the GeoGebra book The Domain of the Time.
This animation simulates the motion of the domino effect in real time. The domino effect behaves like a wave. The leading piece (the wavefront) transmits the falling motion to the next piece, which then becomes the new wavefront. The potential energy lost by each piece as it falls is enough to knock down the next piece. Furthermore, as we will see in the next activity, each piece could even knock down a larger piece.

Each piece of this ideal domino falls following a pendular motion, meaning its top traces an arc of a circle, accelerated by gravity. This ideal behavior assumes the following conditions:
- Each piece cannot move relative to the ground; it can only topple until it collides with the next piece. (In the reality, slight displacements occur.)
- The collisions are completely inelastic (no bouncing). (In the reality, small bounces happen.)
- After hitting the next piece, the piece that struck slides over the other without friction. (In the reality, friction and imbalances occur.)
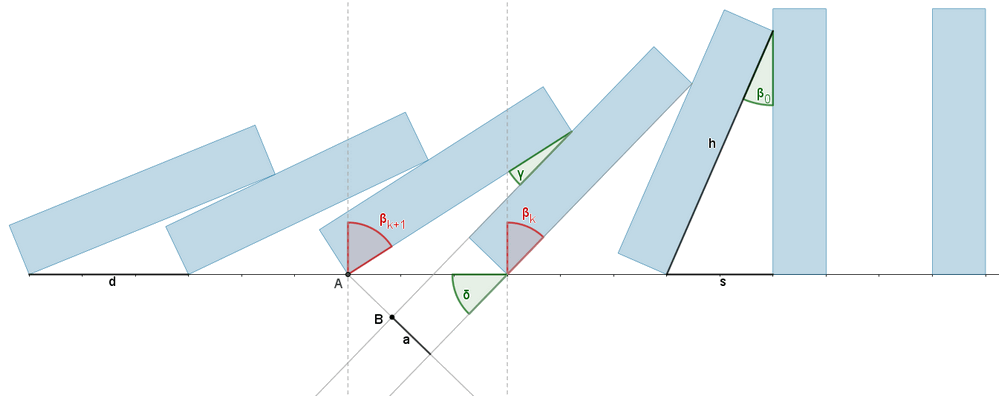
Solving for AB:
and from there:
Therefore, the inclination of each piece is determined by the angle (Mang in the construction) of the leading piece. In turn, this angle of the piece that drags the rest is capped at (Mtrans in the construction):
since beyond this, the next piece becomes the leading one (the angle of the struck piece goes from 0 to , the striking piece's angle goes from to , and so on).
Now, it is enough to define the function:
so that the IterationList command constructs the list of angles ... :
IterationList(f(x), Mang, n)
For better performance, it is recommended to download the GGB file.
SCRIPT FOR SLIDER anima
# Calculate the elapsed seconds dt; add one second if t1(1) < tt
SetValue(tt, t1(1))
SetValue(t1, First(GetTime(), 3))
SetValue(dt, (t1(1) < tt) + (t1(1) − tt)/1000)
# Move M and control the endpoint. The logical value "trans" records the moment of collision with the next piece.
SetValue(M, M + dt v)
SetValue(trans, Mang > Mtrans ∧ N < n)
SetValue(v, If(trans, (x(vt), 0), vt + dt gt))
SetValue(M, If(trans, Rotate((0, h), -Mtrans), M))
SetValue(N, If(trans, N + 1, N))
SetValue(M, If(trans, (0, h) + dt vt, M))
StartAnimation(anima, Mang < angMax || N < n)
Author of the activity and GeoGebra construction: Rafael Losada.