Berechnen von Seitenlängen
Jetzt wollen wir umgekehrt, den Sinus, Kosinus und Tangens nutzen, um Seiten in einem Dreieck zu berechnen.
Die folgenden Übungen zeigen dir, wie das geht.
Im folgenden Beispiel soll die Länge der Seite c ausgerechnet werden, wenn die Winkel und und die Seiten a und b bekannt sind. Dafür löst du nach c auf:
Beispiel 1:
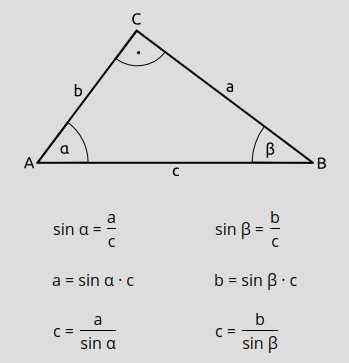
Beispiel 2a)
In einem Dreieck sind die Länge b=7,4 cm und die Winkel =90° und =48,1° gegeben.
Berechne die Länge der Strecke c.
Um die Aufgabe zu lösen, fertigen wir zunächst eine Skizze an:
Skizze:
Rechnung:
Wir stellen einen Zusammenhang auf, in dem c und die gegebenen Größen vorkommen:
bzw.
Löse nun die Gleichung nach c auf.
Multipliziere dazu mit c, damit c nicht mehr im Nenner steht:
und teile durch :
[cm]
Antwort: Die Seite c ist also 9,9 cm lang.
Beispiel 2b)
Wie lang ist in dem Dreieck aus Beispiel 2a) die Seite a? Wir lösen die Aufgabe in mehreren Schritten "gemeinsam". 1. Schritt: Stelle ein Verhältnis auf, in dem a vorkommt. Welches Verhältnis ist richtig?
2. Schritt: Löse schrittweise nach a auf: Welche Gleichung ist hier als Zwischenschritt richtig?
3. Schritt: Löse weiter nach a auf und berechne die Strecke a. Welches Ergebnis ist richtig?

Schriftliche Aufgabe 2:
Berechne in den folgenden beiden Apps A und B die unbekannte Größe.
Verfahre wie im Beispiel, um die Lösung zu berechnen.
Notiere dazu im Heft den Rechenweg.
Du kannst dich in der App am Ende kontrollieren oder dir auch Tipps einholen.
A
B
Noch nicht ganz verstanden?
Dann lass es dir von Lehrer Schmidt erklären! Der kann das! (Du findest das Video ganz unten auf der Seite.)

Schriftliche Aufgabe 3:
Bearbeite schriftlich im Heft:
* S. 176 Nr. 2ab; S. 172 Nr. 5
** Zeichne (mindestens) eines der vier Dreiecke selbst in Geogebra. Miss die Seitenlängen nach, um dich zu kontrollieren. Du kannst in der leeren App hier arbeiten.