Triangles, hauteur et médiatrice - Intro(5e)
Learning Apps - Programme de construction (1)
Définition et caractérisques d'une hauteur dans un triangle (vocabulaire)
En observant la figure ci-dessus, et en déplaçant éventuellement les sommets A, B ou C, choisir la ou les bonne(s) réponse(s)
Learning Apps - Programme de construction (2)
Learning Apps - Hauteurs relatives à un côté dans un triangle
Programme de construction - Tracer des hauteurs
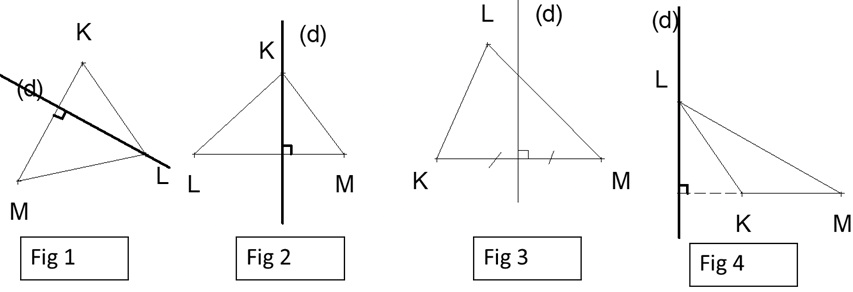
(voir schéma ci-dessus)
Parmi les 4 schémas, quel est l'intrus?
Learning App - Vocabulaire
Construction : Tracer des droites remarquables dans un triangle
Propriétés des hauteurs d'un triangle (1)
(Voir exercice ci-dessus)
Que remarque t’on ?
Propriétés des hauteurs (2) : Déplacer les sommets, puis répondre aux questions ci-dessous
Recopier et compléter le texte suivant sur votre cahier, en vous servant des observations de la figure du dessus
Les trois hauteurs d’un triangle sont concourantes (c’est-à-dire qu’elles…………)
Le point de concours des hauteurs est appelé l’orthocentre du triangle.
L’orthocentre se trouve à l’intérieur du triangle lorsque ……
Il se trouve à l’extérieur lorsque……
Lorsqu’un des angles est droit, l’orthocentre est ……
Learning App - droites remarquables du triangle (QCM)
Learning App - Droites remarquables du triangle (bilan)
Pour travailler de façon autonome (génially)
Pour travailler de façon autonome:
https://view.genially.com/614711492c6ff60ddba8e027/presentation-les-triangles-5e