Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Diagonalen - Satz des Pythagoras

Autor:Gottfried Kendl

Diagonale im Quadrat

Die Diagonale d eines Quadrats mit der Seitenlänge a soll berechnet werden.

   (Ändere den Wert von a im Applet nicht!)

Aufgabe 1a

Um d zu berechnen, bestimmen wir zunächst d2; das ist der Flächeninhalt eines Quadrats mit der Seitenlänge d.

  • Zeichne das "Quadrat über d" ein ("Quadrat" anhaken, aber nicht "Zerlegung").
  • Wie groß ist sein Flächeninhalt im Vergleich zum gegebenen "Quadrat über a"?
  • Wenn du die Frage nicht beantworten kannst, hilft dir die Zerlegung der Fläche (anhaken!).

Antwort überprüfen

Aufgabe 1b

  • Drücke das Ergebnis von Aufgabe 1a als Formel mit den Variablen d und a aus.
  • Löse die Formel nach d auf.

Antwort überprüfen

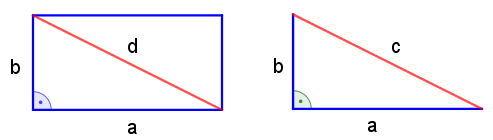
Diagonale im Rechteck

Wir berechnen nun die Diagonale d eines Rechtecks mit den Seitenlängen a und b.  (Ändere jetzt den Wert von a im Applet, sodass das Rechteck kein Quadrat ist!)

Aufgabe 2a

Um d zu berechnen, bestimmen wir zunächst wieder d2; das ist der Flächeninhalt eines Quadrats mit der Seitenlänge d.

  • Zeichne das "Quadrat über d" ein ("Quadrat" und "Zerlegung" anhaken). Die Zerlegung der Fläche enthält jetzt nicht nur Dreiecke , sondern auch ein kleines Quadrat Q.
  • Drücke den Flächeninhalt A1 des Rechtecks und A2 des Quadrats über d durch und Q aus.
  • Drücke den Zusammenhang zwischen A1 und A2 aus.

Antwort überprüfen

Aufgabe 2b

  • Wie groß ist die Seitenlänge s des kleinen Quadrats Q?
  • Drücke das Ergebnis von Aufgabe 2a als Formel mit den Variablen d und a aus.

Antwort überprüfen

Aufgabe 2c

  • Vereinfache die Formel aus Aufgabe 2b.
  • Löse sie nach d auf.  

Antwort überprüfen

Aufgabe 3

Berechne die Länge der Diagonalen (auf eine Dezimale genau): a) Quadrat:  a = 5 cm. b) Rechteck: a = 6 cm, b = 2,5 cm.

Antwort überprüfen

Rechtwinklige Dreiecke

Die Diagonale d im Rechteck ist die Hypotenuse eines rechtwinkligen Dreiecks mit den Katheten a und b. (Die Hypotenuse liegt dem rechten Winkel gegenüber, die Katheten schließen ihn ein.) Wir haben in Aufgabe 2 die Formel für den Zusammenhang zwischen den Katheten und der Hypotenuse bewiesen:



Bezeichnet man die Katheten eines rechtwinkligen Dreiecks mit a, b und die Hypotenuse mit c, so erhält man

Image
Das ist der berühmte Satz des Pythagoras: In jedem rechtwinkligen Dreieck ist die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse.

Neue Materialien

Entdecke Materialien

Entdecke weitere Themen