Cercle inscrit dans un triangle
Tâche
Construire un cercle inscrit dans un triangle
Explorez la construction ci-dessous et découvrez comment inscrire un cercle dans un triangle avec l'application GeoGebra Géométrie. Puis essayez-le vous-même en suivant les instructions ci-dessous.
Explorez la construction....
Instructions
Remarque : Si vous utilisez l'application mobile, assurez-vous que l'option d'étiquetage choisie est Nouveaux points seulement. Vous pouvez modifier cette option en allant dans les Paramètres du menu de l'application et en sélectionnant Général.
| 1. | 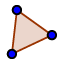 | Créez un triangle ABC avec l'outil Polygone. |
| 2. | 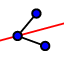 | Sélectionnez l'outil Bissectrice et créez la bissectrice de deux angles du triangle. Conseil : La sélection des trois points A, B et C dans cet ordre produit la bissectrice de l'angle B. |
| 3. |  | Créez l'intersection des deux bissectrices avec l'outil Intersection. |
| 4. | 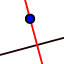 | Sélectionnez l'outil Perpendiculaire puis créez une droite perpendiculaire à un des côtés du triangle et passant par le point D. |
| 5. |  | Créez le point d'intersection E de la perpendiculaire et du côté choisi du triangle à l'aide de l'outil Intersection. |
| 6. | 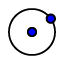 | Sélectionnez l'outil Cercle (centre-point) et construisez le cercle en cliquant sur le point D puis sur le point E. |
| 7. |  | Cachez les lignes auxiliaires créées lors de la construction. |
| 8. |  | Reliez les points D et E à l'aide de l'outil Segment pour afficher le rayon du cercle. |
| 9. |  | Affichez l'angle droit entre le rayon du cercle et le côté correspondant du triangle à l'aide de l'outil Angle. |
| 10. |  | Sélectionnez l'outil Déplacer et faites glisser les sommets du triangle pour vérifier si votre construction est correcte. |