Diagonali di un poligono
TRIANGOLO
Quante diagonali ha un TRIANGOLO?
QUADRILATERO
Quante diagonali ha un QUADRILATERO?
PENTAGONO
Quante diagonali ha un PENTAGONO?
Quante diagonali ha un ESAGONO?
ESAGONO
Quante diagonali ha un ETTAGONO?
ETTAGONO (poligono di 7 lati)
Quante diagonali ha un OTTAGONO?
OTTAGONO
Ecco i nomi dei poligoni in base al numero di lati!
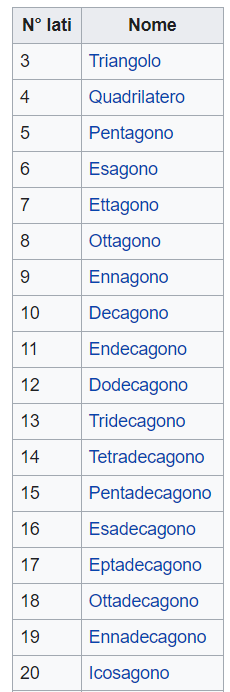
Completa la tabella con i numeri di diagonali che hai trovato.
C'è un legame che intercorre tra il numero di lati e il numero di diagonali di un poligono. Adesso lo scopriamo insieme. Immaginiamo di avere un poligono di n lati. Siccome per tracciare le diagonali congiungi ciascun vertice a tutti i vertici a lui non consecutivi, a quanti vertici congiungi ciascuno degli n vertici?
Però bisogna fare attenzione, così ragionando io conto due volte ciascuna diagonale! La conto una volta congiungendo un vertice a uno non consecutivo e un'altra volta quando faccio il viceversa, vero? Quindi cosa devo fare per non contare due volte ciascuna diagonale?
Quante diagonali ha un poligono di 20 lati?
Quanti lati ha un poligono di 90 diagonali?
Moltiplico per 2 ambo i membri
Sviluppo i calcoli
E' un trinomio speciale come abbiamo imparato stamattina!
Mi servono due numeri che diano come prodotto -180 e come somma -3.
Pensa che -18 e 10 danno come prodotto -180 e come somma -8.
Ci sono problemi di realtà che si possono risolvere con un ragionamento molto simile. In un torneo di calcio ogni squadra gioca una partita contro ogni altra squadra una sola volta. Se in tutto si giocano 120 partite, quante squadre ci sono in tutto?
Se ciascuno di voi stringesse la mano a ciascuno dei suoi 26 compagni, quante strette di mano ci sarebbero in tutto?