Aranyos arányosak (11.)
1. probléma
Van-e olyan paralelogramma, melynek két különböző szögének aránya egyenlő két különböző oldalának arányával?
???
Megoldás:
Bármely a és b oldal esetére van olyan paralelogramma, amely megfelel a feltételeknek.
, .
2. probléma:
Van-e olyan háromszög, mely két szögének aránya egyenlő két oldalának arányával?
Tekintettel arra, hogy a szövegben nem szerepel, hogy melyik szögekről van szó, két lényegesen különböző esetet kell vizsgálni. A szokásos jelölésekkel:
a)
b)
a.)
A szinusztétell szerint a egyenletet kell megoldani a -n az feltétel mellett. A fenti aplettből látszik, hogy a keresett megoldások . (Valószínűleg az egyenletnek nincs algebrai megoldási módszere, a GeoGebra bizonyára numerikus módszerekkel számolt.)b.)
A szinusztétell szerint a egyenletet kell megoldani a -n az feltétel mellett. A fenti aplettből látszik, hogy bármely -hoz egyetlen tejesíti a feltételeket (vélhetőleg ennek az egyenletnek sincs algebrai megoldási módszere, a GeoGebra bizonyára numerikus módszerekkel számolt.)3. probléma
Van-e olyan szimmetrikus trapéz, melynek két szögének aránya az alapok arányával egyenlő?
???
Az applet szerint minden 0 < c < a esetén van ilyen trapéz. Tekintettel arra, hogy a trapéz egy szárán fekvő szögek összege egyenesszög, a szögek: , .
4. probléma
Van-e olyan trapéz, amelyek oldalainak aránya egyenlő a szögeik arányával?
Megoldás:
Az 1. problémában láttuk, hogy ilyen paralelogramma létezik. Ebből következően a nem paralelogramma trapézokat kell vizsgálni.
A trapéz szárain levő szögek összege egyenesszög, akkor annak, hogy az oldalak aránya egyenlő legyen a szögek arányával, szükséges feltétele, hogy a trapéz két-két oldalának összege egyenlő legyen.
Két eset lehetséges:
a) A trapéz szárainak összege egyenlő az alapok összegével.
b) Az egyik alap és az egyik szár összege egyenlő a másik alap és a másik szár ősszegével.
a.) Keressünk egy ilyen trapézt!
d(a) függvény
A fenti grafikon a GeoGebra CAS (komputeralgebrai rendszer) alkalmazásával készült. Az ABD és a BCD háromszögekben alkalmazott koszinusztétel segítségével adja az d(a) függvényt (piros színű grafikon). A feltételek:
b.)
A fenti applet alapján bizonyíthatjuk, hogy, ha egy trapéz egyik alapjának és egy szárának összege egyenlő a másik alapjának ée szárának összegével, akkor az paralelogramma.
5. probléma
Van-e olyan deltoid, amely két oldalának aránya egyenlő lét szögének arányával?
Tekintsük a következő ábrát!
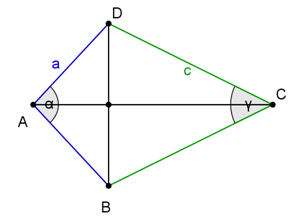
Két eset lehetséges:
a.)
b.) aaa
a.)
Ezt az egyenletet kell megoldani a -n.A CAS-szal kapott ábra
Úgy tűnik, hogy csak az megoldás, tehát a négyszög rombusz.
b.)
A megoldást a -n keressük.A GeoGebra CAS ezt adja:
További kérdés
Van-e olyan egyéb négyszög, amely oldalainak aránya egyenlő a szögeinek arányával?
Játsszunk egy kicsit!
A csúszkák mozgatásával érjük el, hogy a D és T pontok egybe essenek!