Dokumentation: Symmetriebegriff

Symmetrie. Ein Thema, dem wir alle schon begegnet sind und mit dem wir tagtäglich in Kontakt kommen. Jeder Mensch assoziiert etwas anderes mit dem Begriff "Symmetrie". Unabhängig von unseren konkreten Assoziationen, ist jedoch das positive Empfinden, welches sich automatisch bei diesem Thema einstellt. Egal, ob wir an Blumen, Schmetterlinge und Menschen oder an Verkehrsschilder, Flaggen, Logos und Mandalas denken: Symmetrie tritt in allen Bereichen des Lebens auf und wirkt auf uns ansprechend. Diese Tatsache ist ein enormer Vorteil beim Einführen und Behandeln des Themas "Symmetrie" im Mathematik-Unterricht, denn die Schülerinnen und Schüler können aufgrund ihrer vielfältigen Alltagserfahrungen direkt in ihrer eigenen Erfahrungswelt abgeholt werden. (vgl. [1]) Aber wie ist "Symmetrie" überhaupt definiert? Das Wort "Symmetrie" kommt aus dem Altgriechischen und bedeutet übersetzt "Ebenmaß" oder "Gleichmaß". (vgl. [2]) Wenn man aus mathematischer Sicht an den Symmetriebegriff herangeht, denkt man sofort an Achsensymmetrie und Punktsymmetrie. Zusätzlich zu diesen beiden Symmetriearten gibt es noch die Dreh- bzw. Rotationssymmetrie und die Verschiebungssymmetrie. Bei der Auseinandersetzung mit Symmetrien fällt außerdem auf, dass es zwei unterschiedliche Herangehensweisen an das Thema gibt. Zum einen kann Symmetrie als Eigenschaft geometrischer Figuren gesehen werden, zum anderen kann man den Abbildungsaspekt in den Vordergrund stellen. Die vier Arten von Symmetrien werden in der Fachliteratur mithilfe des Abbildungsaspekts und des Begriffs der Spiegelung definiert (vgl. [3]):

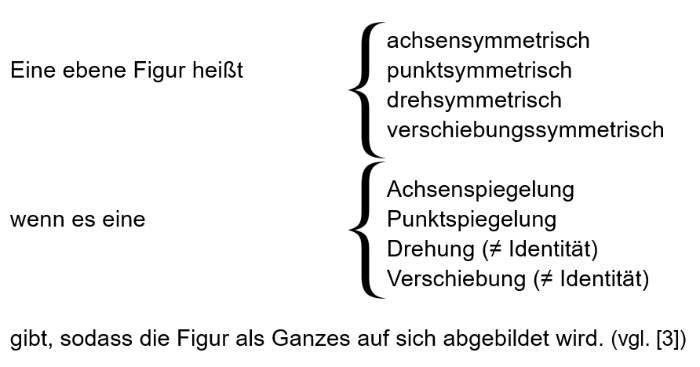
Wichtig ist hierbei zu beachten, dass der Spiegelbegriff ein Teil der Symmetriedefinition ist und somit diese beiden Themenfelder untrennbar miteinander verbunden sind. Im Folgenden soll auf die fachdidaktischen Hintergründe des Symmetriebegriffs eingegangen werden. Zum einen ist es wichtig den Schülerinnen und Schülern die zwei wichtigen Sichtweisen auf Symmetrien zu vermitteln: die statische Definition (Lage von Punkten) und die dynamische Definition (Invarianz bei Abbildungen, Abbildungseigenschaften). (vgl. [1]) Zum anderen ist im Sinne des Spiralprinzips nach Jerome Bruner die Reihenfolge der zu vermittelnden Lerninhalte wichtig. Um den Lernerfolg zu garantieren, müssen die Inhalte strikt aufeinander aufbauen und folgende Grundsätze beachtet werden:

• Die bereits gelernten Inhalte und Kompetenzen werden wiederholt. 
• Es folgt die Erarbeitung neuer Aspekte und Lernziele. Dabei kommt es zu einer Steigerung des Niveaus.
• Das Gelernte wird kontinuierlich ausgebaut und vertieft. (vgl. [4])

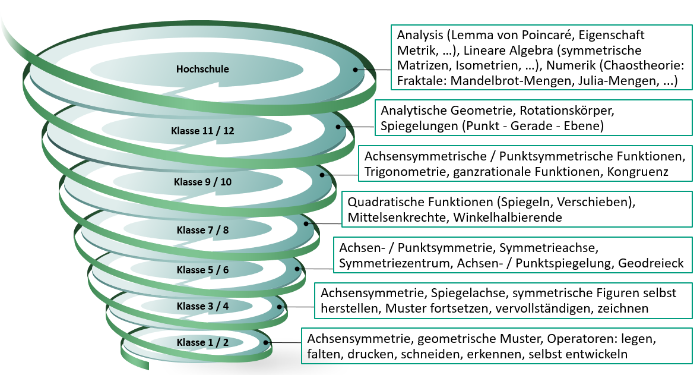
Das Thema Symmetrie ist in den Klassen 1-6 der Leitidee "Raum und Form" zugeordnet, ab Klasse 7/8 tritt es zusätzlich im Leitmotiv "Funktionaler Zusammenhang" auf. (vgl. [5] und [6]) Beim Vergleich mehrerer Schulbücher ist die unterschiedliche Aufbereitung des Themas Symmetrie auffällig. Im "Lambacher Schweizer Klasse 5" (Klett-Verlag, 2014) werden beispielsweise für die Themen Achsen- und Punktsymmetrie nur sieben Seiten zur Verfügung gestellt. Der Einstieg erfolgt hier über Aufgaben zur Spiegelung. Anschließend folgen Aufgaben zu Symmetrieeigenschaften, wie zum Beispiel das Einzeichnen von Symmetrieachsen. (vgl. [7]) Als Alternative dazu gibt es zum Beispiel das Lehrbuch "Elemente der Mathematik Klasse 6" (Schroedel-Verlag, 2015), welches insgesamt fünfzehn Seiten mit Aufgaben zur Achsen- und Punktsymmetrie füllt. Die Reihenfolge der Aufgaben ist im Vergleich zum oben genannten Lambacher Schweizer umgedreht: zuerst werden Symmetrieeigenschaften behandelt, erst danach folgen die Spiegelungen. (vgl. [8]) Unabhängig vom eingeführten Schulbuch ist es wichtig, bei der Unterrichtsvorbereitung mehrere Bücher zur Hand zu nehmen. Jedes Lehrbuch hat seine Stärken und Schwächen und je nach Lernstand und Lernzielen bedarf es anderer Inhalte und Aufgabenstellungen. Außerdem müssen beim Konzipieren von Übungs- bzw. Prüfungsaufgaben verschiedene Faktoren bezüglich des Schwierigkeitsgrads von den Lehrkräften beachtet werden. Dieser lässt sich beispielsweise variieren durch:

• die Lage der Spiegelachse (senkrechte/waagrechte Achse deutlich leichter als schrägliegende Achse)
• das zur Verfügung gestellte Papier (Spiegeln auf Karopapier oft leichter als auf Blankopapier) (vgl. [9])

Im Allgemeinen sollte zur Bearbeitung der Aufgaben genügend Platz auf dem Papier zur Verfügung stehen, um Lösungen nicht vorweg zu nehmen. Zudem kann es hilfreich und abwechslungsreich sein digitale Lehrmittel zu verwenden, wie beispielsweise Apps oder GeoGebra. Ein Beispiel für eine App, die durchaus für den Mathematik-Unterricht geeignet ist, ist die ANTON-App. Diese bietet von der Vorschule bis zum Abitur viele Aufgaben zur Übung und Vertiefung an und ist unabhängig vom jeweiligen Bundesland einsetzbar. Die ANTON-App ist kostenlos, sehr übersichtlich und kinderfreundlich gestaltet. Daher eignet sie sich sowohl zur Überprüfung der erreichten Kompetenzen, als auch für Hausaufgaben oder zum Selbsttraining für die Schülerinnen und Schüler. Die Lehrkraft kann die zu bearbeitenden Aufgaben gezielt dem Unterricht anpassen und von den Schülerinnen und Schülern erreichte Ergebnisse einsehen. (vgl. [10] und [11]) Ein Beispiel für ein GeoGebra-Applet, welches sich zum Einsatz im Mathematik-Unterricht eignet, ist das Folgende von Hubert Pöchtrager. Hierbei sollen die gegebenen Verkehrsschilder dem entsprechenden Bereich zugeordnet werden. Wenn alle Schilder richtig zugeordnet wurden, erscheint ein Smiley. Verkehrsschilder sind ein Beispiel aus unserem Alltag. Somit werden die Schülerinnen und Schüler wie anfangs bereits beschrieben direkt in ihrer Erfahrungswelt abgeholt und haben dadurch einen direkten und intuitiven Zugang zur Aufgabenstellung. (vgl. [12]) Sowohl beim Einsatz der ANTON-App, als auch beim Arbeiten mit dem GeoGebra-Applet ergibt sich ein zusätzlicher Übungsanreiz aufgrund des Methodenwechsels. Die Schülerinnen und Schüler üben den Umgang mit digitalen Werkzeugen und verbessern so ihre Medienkompetenz.

Im Allgemeinen gilt es jedoch vor jeder Übung die Stärken bzw. Schwächen von analogen und digitalen Arbeitsmethoden abzuwägen und dann das besser geeignete Tool zur Verfügung zu stellen. So ist es zum Beispiel wichtig, handwerkliche Kompetenzen wie den Umgang mit dem Geodreieck, analog zu üben. Unabhängig davon, ob die Schülerinnen und Schüler analog oder digital arbeiten, kann man schlussfolgern, dass der Spaß am entdeckenden Lernen mithilfe beider Arbeitsmethoden gut gefördert werden kann. Je nach Lernziel und je nach Aufgabenstellung bieten sich unterschiedliche "Arbeitswelten" an!