Elipses como composición de funciones
Con los ejercicios anteriores hemos visto que componiendo la función circular con funciones afines tanto por la derecha como por la izquierda se consiguen semielipses.
Por ejemplo, si quisiéramos expresar la elipse centrada en (-3,2) y de semiejes 2 y 1, podemos obtener dos funciones (una para la semielipse superior y otra para la inferior) a partir de composiciones como se muestra a contimuación:
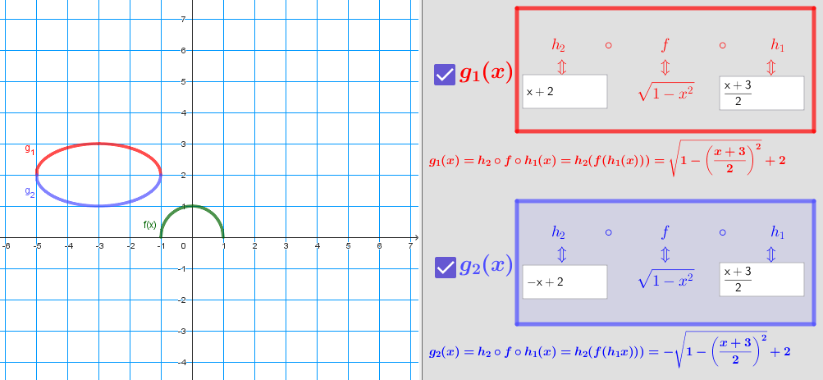
En el siguiente applet puedes introducir la expresión analítica de las funciones y tanto para la semielipse superior () como para la inferior ().
EJERCICIO 1
Indica qué curva forman la gráficas de las funciones: y
EJERCICIO 2
Obtén dos funciones cuyas gráficas formen una elipse centrada en (3,-3) de semiejes 4 y 2.
EJERCICIO 3
Obtén dos funciones cuyas gráficas formen una elipse centrada en (-2,4) de semiejes y 3.
EJERCICIO 4
Obtén dos funciones cuyas gráficas formen una circunferencia centrada en (2,5) de radio 3.