Torre Espacio
Situada en la denominada Cuatro Torres Business Area se encuentra la Torre Espacio. Tiene una altura de 224 metros y 57 plantas sobre el nivel del suelo. Su construcción comenzó en 2004 y finalizó en marzo de 2007.

Un simple vista a pie de calle nos muestra la grandiosidad de este edificio. Un análisis más detallado nos muestra sus peculiaridades, tiene una base cuadrada que poco a poco se va transformando, el perfil del edificio parece describir una curva conforme el número de plantas asciende y termina en forma “semicircular”.
En este punto podemos recurrir a la ortofoto y observar que el edificio que comienza con cuatro caras formando un cuadrado en la planta baja termina con dos caras formadas por dos cuartos de circunferencia en la planta 57.
La primera vez que observas este edificio se acumulan las preguntas: ¿habrá alguna relación entre la base y la azotea? ¿Cuál será la curva que parece describir el perfil de la fachada? ¿Cómo conseguir curvar el edificio respetando las escaleras de incendio? Estas preguntas y otras muchas suelen ser el detonante para proponer el estudio de la geometría del edificio.
Matemáticamente podemos ver la torre como un prisma cuadrado de altura 235 metros. En este prisma tenemos dos restricciones que son la escaleras de incendio, dos primas cuadrados contenidos dentro del edificio y situados en "vértices opuestos".
¿Cómo conseguir curvar el edificio respetando las escaleras de incendio?
Obviamente el diseño de la fachada depende de la altura. Una exploración in situ muestra que en las seis primeras plantas no se produce ninguna acción, es decir, son rectas. Es a partir de la planta número 7 cuando observamos que la fachada se va curvando. Esta forma de curvar la fachada es lo que caracteriza a la Torre Espacio y es matemáticamente una idea muy simple, constructivamente no tanto.
Partiendo de un cuadrado base con sus dos escaleras de incendio:
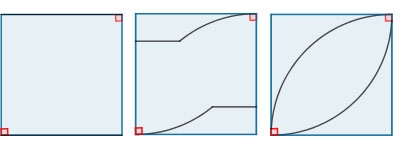
Debemos iniciar un arco que irá creciendo en cada planta hasta completar el cuarto de vuelta en la última planta.
Podemos modelizar con los alumnos las diferentes plantas del edificio. Casi sin darnos cuenta, GeoGebra nos ofrece la posibilidad de pasarnos a 3D e intentar obtener un modelo tridimensional del edificio.