1.2.2 The Velocity Vector
The two vectors defined in the previous activity were either always horizontal () or always vertical (). One appeared to change directions periodically while the other never did. The gifs below illustrate both vectors. Explain.
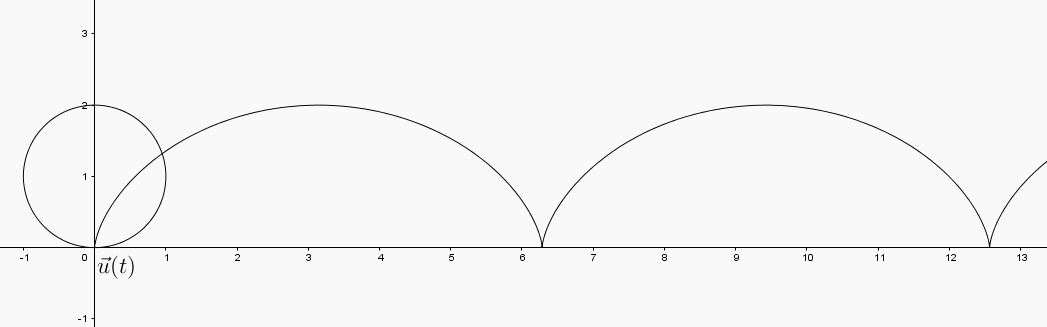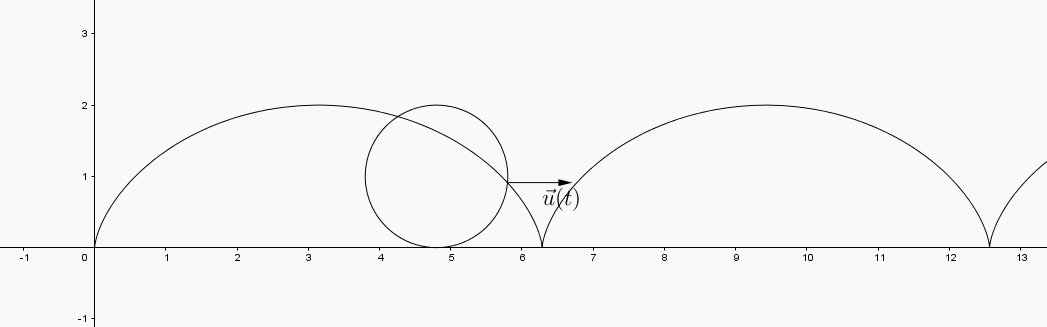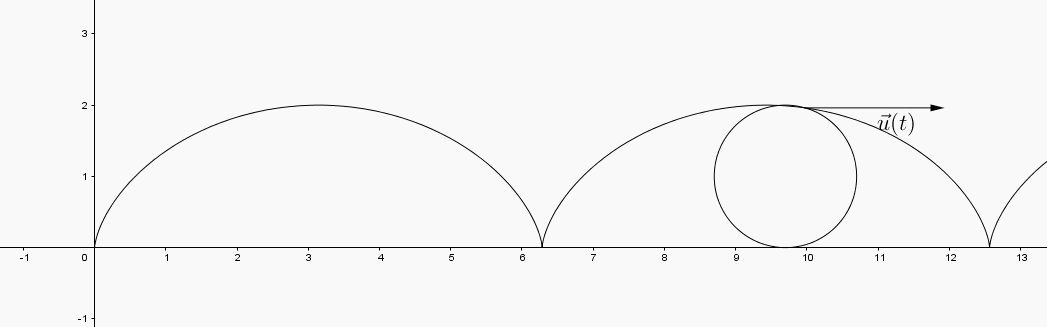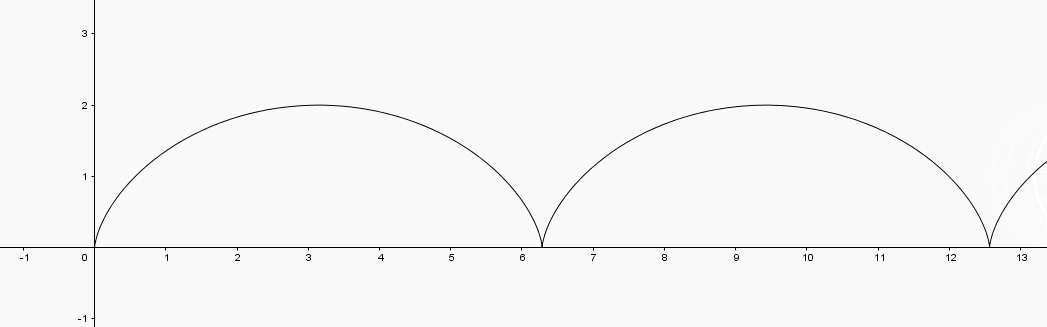
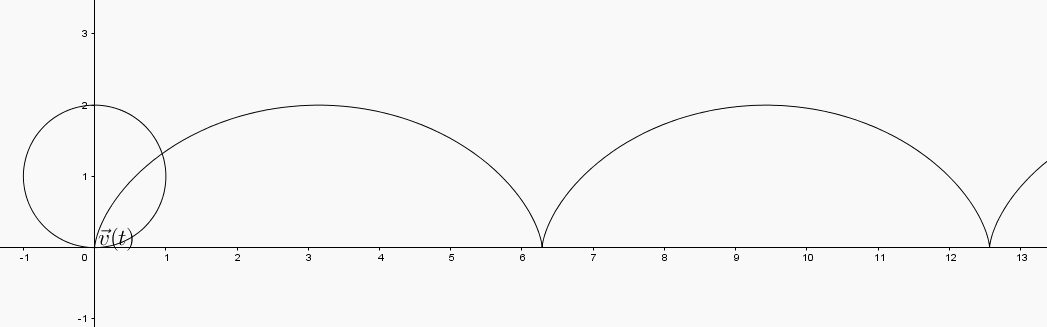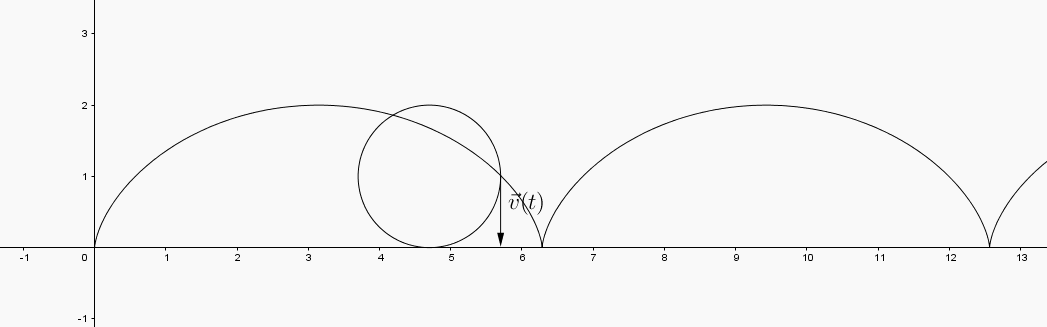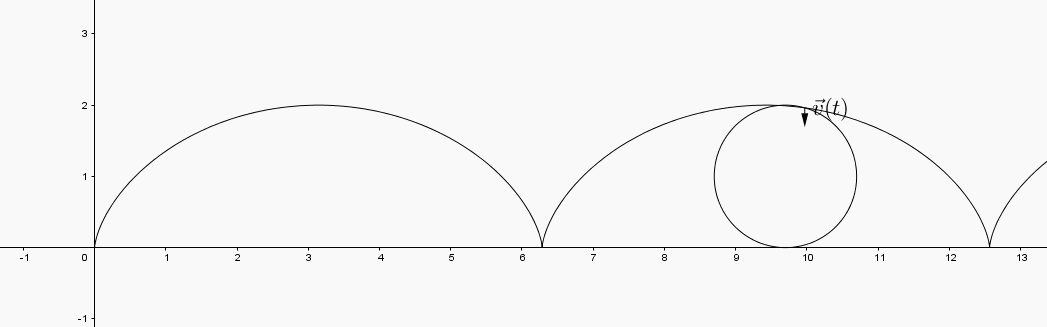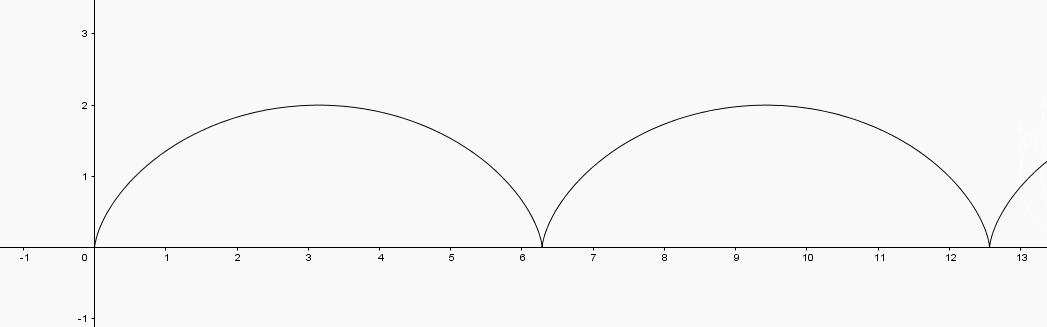
The sum of these two vectors is the velocity vector to the path . That is, the velocity vector to the path is the vector .
With this new vocabulary word we can rewrite the definition of differentiable and regular:
- A differentiable path is a function for which exists at every point in the domain. (path property)
- A differentiable curve is one for which there is a differentiable parameterization. (curve property)
- A regular path is one for which exists and is never at any point in the domain. (path property)
- A differentiable path is said to be of class if the derivatives of the component functions are continuous.
- A path whose component functions are -times differentiable with all derivatives continuous is said to be of class .
- A path whose component functions are infinitely differentiable with all derivatives continuous functions is said to be of class or sometimes such a path is said to be smooth.
In the GeoGebra applet below you can view the interactions between the vectors
and the velocty vector .
changes length. Where is the length of maximized? minimized? What is happening in the image curve at these points? appears to swivel in a way that the horizontal and vertical vectors did not. What does the direction of the vector tell you about the path?