Area Under the Curve
Reflection on Area Under the Curve
The area under a curve between two points can be found by doing a definite integral between the two points. To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b. Areas under the x-axis will come out negative and areas above the x-axis will be positive.
Area Under a CurveCalculating the area under a curve. Definite IntegralsSo far when integrating, there has always been a constant term left. For this reason, such integrals are known as indefinite integrals. With definite integrals, we integrate a function between 2 points, and so we can find the precise value of the integral and there is no need for any unknown constant terms [the constant cancels out].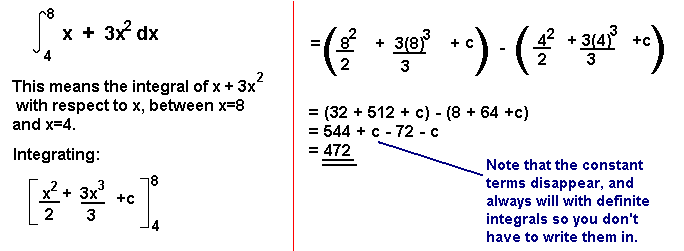
The Area Under a CurveThe area under a curve between two points can be found by doing a definite integral between the two points.To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b.
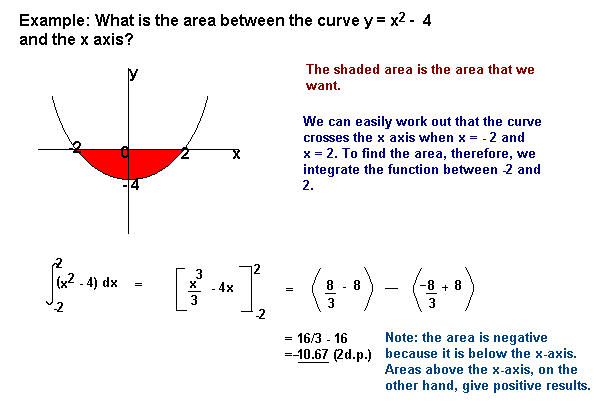Areas under the x-axis will come out negative and areas above the x-axis will be positive. This means that you have to be careful when finding an area that is partly above and partly below the x-axis.
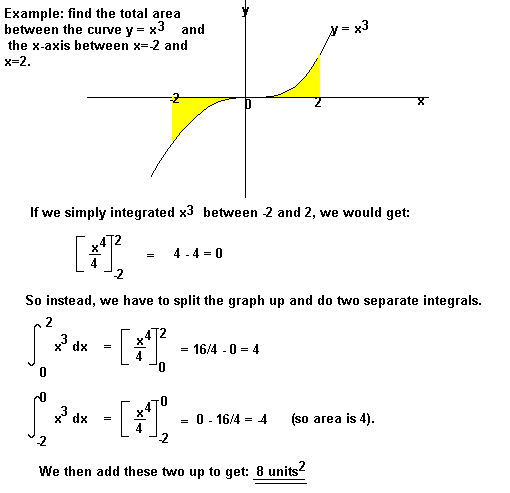You may also be asked to find the area between the curve and the y-axis. To do this, integrate with respect to y.ExampleFind the area bounded by the lines y = 0, y = 1 and y = x2.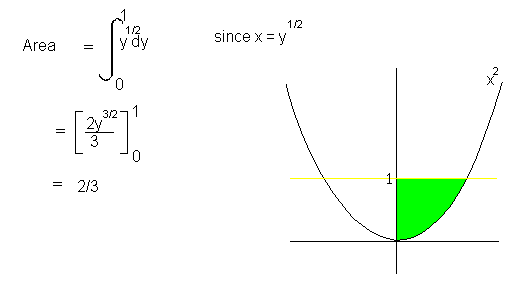
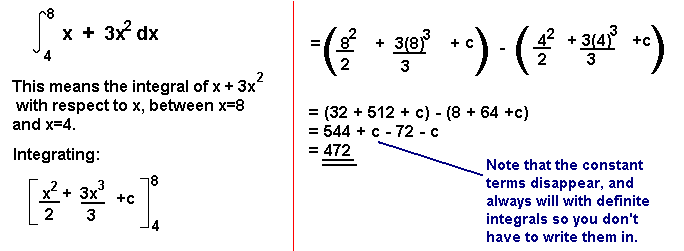The Area Under a CurveThe area under a curve between two points can be found by doing a definite integral between the two points.To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b.Areas under the x-axis will come out negative and areas above the x-axis will be positive. This means that you have to be careful when finding an area that is partly above and partly below the x-axis.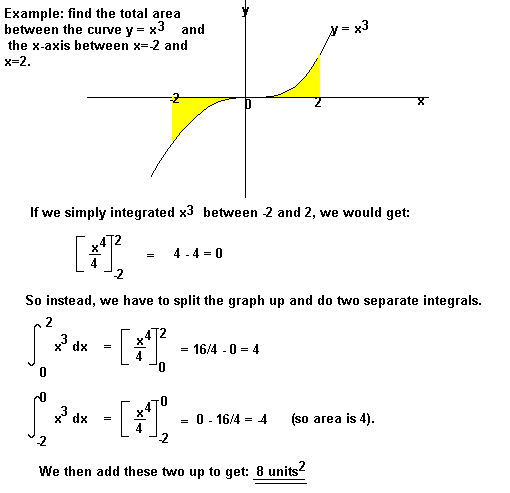You may also be asked to find the area between the curve and the y-axis. To do this, integrate with respect to y.ExampleFind the area bounded by the lines y = 0, y = 1 and y = x2.