Cicloide
Wilfred Gottfried Leibniz (1646-1716), en su estudio del Cálculo Infinitesimal, demostró que curvas que no habían podido adquirir hasta ese momento una expresión analítica, como las denominadas curvas mecánicas de Viète y Descartes, podían adquirirla a partir de sus métodos analíticos y su notación. Por ejemplo, dio la primera ecuación compacta de la cicloide. Leibniz trató la curvatura, definió el concepto de la circunferencia osculatriz (mal llamada círculo osculador) y desarrolló en buena parte la teoría de envolventes.

Cómo programarla en Geogebra como lugar geométrico
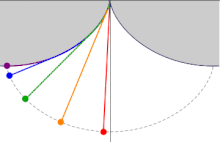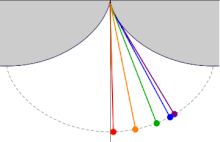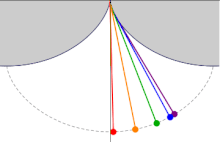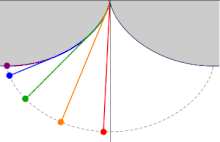
La cicloide es la curva braquistócrona
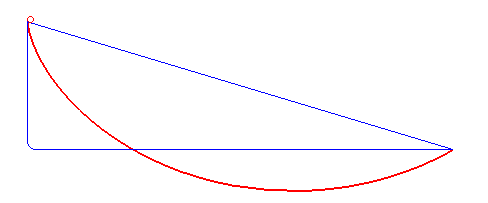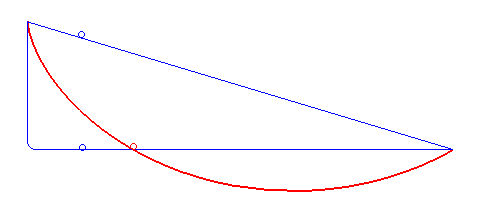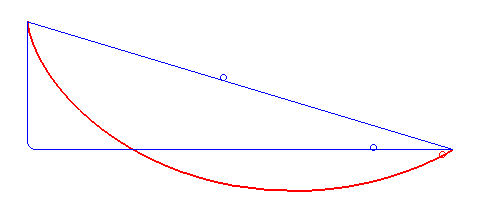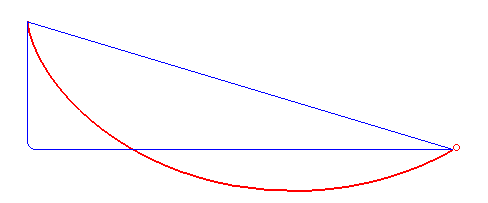
Es bien sabido que la trayectoria recta es la que minimiza la distancia (euclídea) entre dos puntos del espacio o del plano; sin embargo, ¿es esta trayectoria la que minimiza el tiempo que tarda una partícula en ir entre dichos dos puntos? Una curva braquistócrona (gr. βράχιστος brachistos 'el más corto', χρόνος chronos 'intervalo de tiempo'), o curva del descenso más rápido, es la curva entre dos puntos que es recorrida en menor tiempo por un cuerpo que comienza en el punto inicial con velocidad cero y que debe desplazarse a lo largo de la curva hasta llegar al segundo punto, bajo acción de una fuerza de gravedad constante y suponiendo que no existe fricción. En la solución del problema intervinieron, entre otros, Johann y Jakob Bernoulli, Leibniz, L'Hôptial y Tschirnhaus. Finalmente, el 24 de enero de 1697, Newton resolvió el problema de la braquistócrona (en lo que fue el primer resultado en el cálculo de variaciones --rama de la matemática consistente en buscar extremos relativos de funcionales continuos definidos sobre algún espacio funcional--): la cicloide daba la solución. Dados dos puntos A y B, con A a una elevación mayor que B, existe solo una curva cicloide con la concavidad hacia arriba que pasa por A con pendiente infinita (dirección vertical y sentido de arriba hacia abajo), también pasa por B y no posee puntos máximos entre A y B. Esta particular cicloide invertida es la curva braquistócrona. La curva no depende de la masa del cuerpo o del valor de la constante gravitacional. No obstante, si al cuerpo se le da una velocidad inicial en A, o si se toma en cuenta el efecto de la fricción, la curva que minimiza el tiempo de tránsito será distinta de la descrita.
La cicloide es la curva braquistócrona
Huygens y los relojes de péndulo
La cicloide es la curva tautócrona
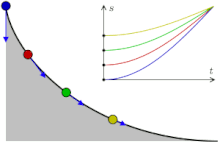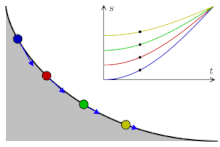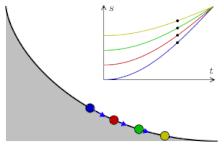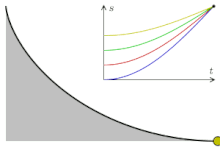
La evoluta de la cicloide es otra cicloide, pero desplazada. Y es la curva tautócrona.