Longitud de arco
LONGITUD DE ARCO
La longitud de arco es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. Las primeras mediciones se hicieron posibles a través de aproximaciones trazando un polígono dentro de la curva y calculando la longitud de los lados de éste para obtener un valor aproximado de la longitud de la curva. Mientras se usaban más segmentos, disminuyendo la longitud de cada uno, se obtenía una aproximación cada vez mejor.
En aplicaciones anteriores de integración, requeríamos quef(x)�(�) la función fuera integrable, o como mucho continua. Sin embargo, para calcular la longitud del arco tenemos un requisito más estricto paraf(x)�(�). Aquí, requerimosf(x)�(�) ser diferenciables, y además requerimos que su derivado,f'(x),�′(�), sea continuo. Funciones como esta, que tienen derivadas continuas, se llaman lisas. (Esta propiedad vuelve a aparecer en capítulos posteriores.)
Dejarf(x)�(�) ser una función suave definida sobre[a,b][�,�]. Queremos calcular la longitud de la curva desde el punto(a,f(a))(�,�(�)) hasta el punto(b,f(b))(�,�(�)). Comenzamos usando segmentos de línea para aproximar la longitud de la curva. Parai=0,1,2,…,n�=0,1,2,…,�, dejarP=xi�=�� ser una partición regular de[a,b][�,�]. Después, parai=1,2,…,n�=1,2,…,�, construya un segmento de línea desde el punto(xi−1,f(xi−1))(��−1,�(��−1)) hasta el punto(xi,f(xi))(��,�(��)). Aunque pueda parecer lógico usar segmentos de línea horizontales o verticales, queremos que nuestros segmentos de línea se aproximen lo más posible a la curva. La figura6.4.16.4.1 representa este constructo paran=5�=5.
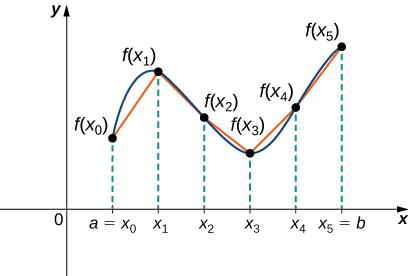Figura6.4.16.4.1: Podemos aproximar la longitud de una curva sumando segmentos de línea.Para ayudarnos a encontrar la longitud de cada segmento de línea, observamos el cambio en la distancia vertical así como el cambio en la distancia horizontal en cada intervalo. Debido a que hemos utilizado una partición regular, el cambio en la distancia horizontal sobre cada intervalo viene dado porΔxΔ�. Sin embargo, el cambio en la distancia vertical varía de un intervalo a otro, por lo que usamosΔyi=f(xi)−f(xi−1)Δ��=�(��)−�(��−1) para representar el cambio en la distancia vertical a lo largo del intervalo[xi−1,xi][��−1,��], como se muestra en la Figura6.4.26.4.2. Tenga en cuenta que algunos (o todos)ΔyiΔ�� pueden ser negativos.
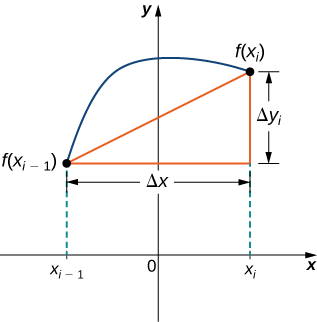Figura6.4.26.4.2: Un segmento de línea representativo se aproxima a la curva a lo largo del intervalo[xi−1,xi].[��−1,��].Según el teorema de Pitágoras, la longitud del segmento de línea es
Figura6.4.16.4.1: Podemos aproximar la longitud de una curva sumando segmentos de línea.Para ayudarnos a encontrar la longitud de cada segmento de línea, observamos el cambio en la distancia vertical así como el cambio en la distancia horizontal en cada intervalo. Debido a que hemos utilizado una partición regular, el cambio en la distancia horizontal sobre cada intervalo viene dado porΔxΔ�. Sin embargo, el cambio en la distancia vertical varía de un intervalo a otro, por lo que usamosΔyi=f(xi)−f(xi−1)Δ��=�(��)−�(��−1) para representar el cambio en la distancia vertical a lo largo del intervalo[xi−1,xi][��−1,��], como se muestra en la Figura6.4.26.4.2. Tenga en cuenta que algunos (o todos)ΔyiΔ�� pueden ser negativos.
Figura6.4.26.4.2: Un segmento de línea representativo se aproxima a la curva a lo largo del intervalo[xi−1,xi].[��−1,��].Según el teorema de Pitágoras, la longitud del segmento de línea es