Fresnel-Zonen Konstruktion für Spaltbeugung.
Fresnel-Zonen Konstruktion (oder abgekürzt FZK) für Spaltbeugung.
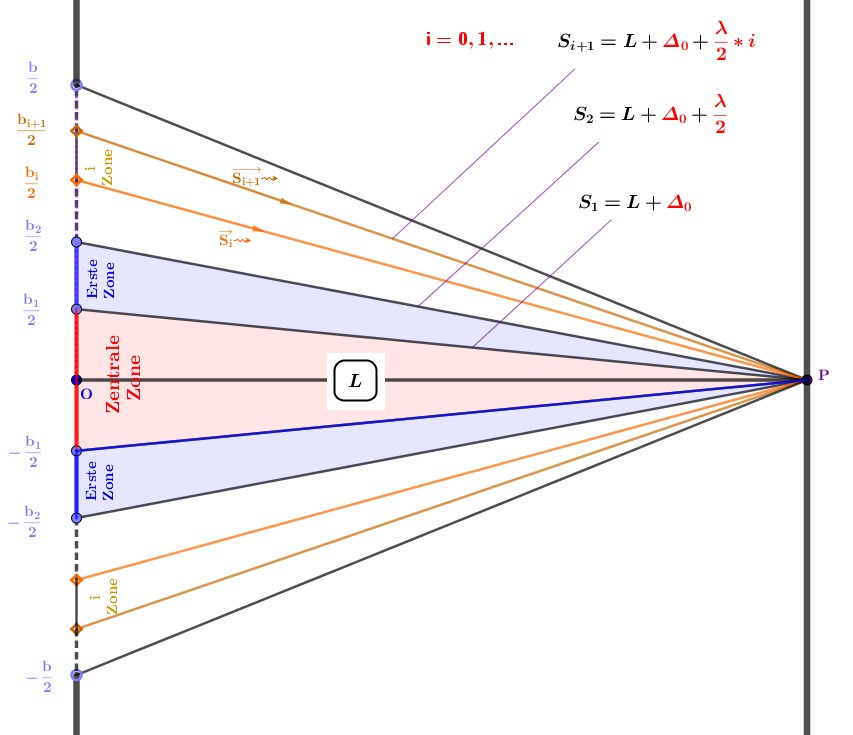
Die Idee der Fresnel-Zonen Methode (wird zur Erklärung der Beugung an einer kreisförmigen Öffnung verwendet) erweist sich als anwendbar auf den Fall eines Spalts: Die ebene Wellenfront ist in Halbwellenzonen unterteilt, die von Schuster eingeführt wurden und analog zu den Fresnel-Zonen sind, aber im Gegensatz zu diesen allmählich an Fläche abnehmen. Die Längsachse des Spalts, die durch den Punkt O verläuft, teilt die zentrale Zone in zwei Teile. Die Zonen oberhalb von O sind mit 0, 1, 2 usw. nummeriert, die Zonen unterhalb mit 0', 1', 2' usw. Es ist klar, dass die Breite (und die Fläche) der Zonen mit den Nummern m und m' gleich sind, so dass die Lichtschwingungen, die sie im Punkt P erzeugen, die gleiche Amplitude und Phase haben. Die Zonenunterteilung erfolgt, indem sie von den Grenzen der ersten und zweiten Zone ausgehend λ/2 sequenziell dem Abstand L vom Beobachtungspunkt P zu den Zonengrenzen hinzufügt.
In diesem Applet (zur Berücksichtigung der Beugung hinter dem Spalt) wird die Konstruktion von Fresnel-Zonen in Form von vielen Spalten (statt kreisförmiger Fresnel-Zonen bei Beugung hinter Lochblende) durchgeführt. Im Gegensatz zur Schuster-Methode (um auch die Beugung hinter dem Spalt zu berücksichtigen) werden nur die Abstände von den Grenzen der zentralen Zone bis zum Punkt P: L+Δ0, wo der Zusatz (wie die Berechnungen zeigen) Δ0≠λ/2 . Bezeichnen wir diesen Zusatz als den "anfänglichen" Gangunterschied.
In dem interaktiven Applet finden Sie die Intensitätsverteilung des Beugungsfeldes auf der Spaltachse durch numerische Berechnung des Beugungsintegrals nach dem Huygens-Fresnel-Prinzip und den Aufbau der Fresnel-Zonen in Form von vielen Spalten in Abhängigkeit von der Lage des Beobachtungspunktes auf der Spaltachse. Sie werden in der Lage sein, die Genauigkeit der Bestimmung der Positionen der Extrema der Funktion I=I(x) mit Hilfe der Zonenkonstruktion abzuschätzen, d.h. ohne die Notwendigkeit, Beugungsintegrale zu berechnen.
Wir betrachten eine ebene monochromatische Welle (Wellenlänge λ), die auf einen Spalt variabler Breite senkrecht fällt (Applet).
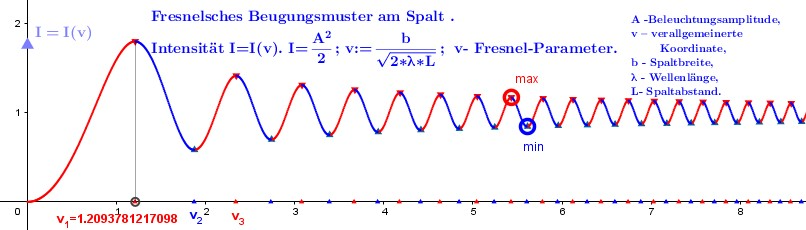
Vergrößern wir den Spalt und beobachten wir die Lichtinterferenz auf der Spaltachse am Punkt P im Abstand L (Abstand zwischen Spalt und Schirm) von ihm (Abb.1). Wir suchen die Extremwerte der Lichtintensitätsverteilungsfunktion an diesem Punkt als Funktion des Parameters v=b/sqrt(2*λ*L), ausgedrückt in Einheiten, die umgekehrt zur Entfernung L sind. Es handelt sich um eine oszillierende Funktion (Abb.2). Das erste Maximum v1 und dementsprechend die Spaltenbreite b1=v1*sqrt(2*λ*L), bei der das erste Maximum im Punkt P erreicht wird. Die Koordinaten des Spaltes sind in diesem Fall (-v1/2,v1/2) oder (-b1/2,b1/2). Spalt stellt in diesem Fall, bezogen auf den Beobachtungspunkt P, die zentrale Zone dar und v1≙F1 ist der -erste Brennpunkt. Der Gangunterschied zwischen den Strahlen, die sich von jedem Ende der Zone ausbreiten, und dem Strahl entlang der Längsachse des Spalts, der zum Brennpunkt F1 konvergiert, wird als Δ0 bezeichnet. Sie lässt sich aus der Geometrie der Konstruktion ableiten: Δ0=sqrt(b12/4+F12)-F1. Sie ist abhängig von der Wellenlänge und Spaltbreite und muss (im Gegensatz zu Schusterzonen) für jedes Verhältnis b/λ numerisch berechnet werden. Konstante Δ0≠ (im Gegensatz zu Fresnel'sche Zonenkonstruktion bei einer kreisförmigen Öffnung!).
Wenn wir den Spalt weiter vergrößern, dann beobachten wir bei einer bestimmten Breite (-b2/2,b2/2) bereits das Minimum am Punkt P. Der hinzugefügte Teil von Spalt ist also die erste Zone. Am Punkt P wird bereits der zweite Fokus v2≙F2 beobachtet - das Minimum der Intensitätsverteilung. Ermitteln wir die Gangunterschied zwischen den Strahlen von verschiedenen Rändern dieser Zone: Δ1=sqrt(b22/4+F22)-sqrt(b1^2/4+F12). Der Gangunterschied beträgt hier, wie auch für andere Nachbarzonen, laut Bauschema λ/2! Wie numerische Berechnungen des Beugungsintegrals zeigen, sind die gefundenen Brennpunkte v1, v2, v3,... bzw. F1, F2,F3, ... (mit hoher Genauigkeit) Extrema der Verteilungsfunktion der Intensität des Beugungsfeldes entlang der Spaltachse. Dies ist auch hier die Begründung für die "Halbwellenzonen"-Methode!!!
Man kann den verallgemeinerten Fresnel-Parameter auch so interpretieren, dass man die Spaltgröße b festlegt und die Bildung der Abhängigkeit I=I(v) als einen Prozess von Intensitätsänderungen nicht an einem Punkt P, sondern an verschiedenen Punkten entlang der Spaltenachse (x-Achse, Extremwerte: F1, F2, ...) betrachtet (Applet).
Im allgemeinen Fall hängt das Beugungsintegral vom Verhältnis bλ:= ab: die Anzahl der Extrema ist gleich diesem Verhältnis (abb.3 und Abb.4). In der Fresnel-Näherung ist das Beugungsintegral unabhängig von den Werten dieses Parameters, so dass die v-Extreme der Lichtintensitätsverteilung eindeutig bestimmt sind (Abb. 2). Die Anzahl der v-Extrema ist in diesem Fall unendlich.. Mit Hilfe der nachfolgenden Applets können Sie diese Aussage überprüfen.
![[size=85][b]Abb.3[/b] Verteilung der Lichtintensität hinter einem Spalt entlang der Spaltenachse als Funktion des Fresnelschen v-Parameters durch numerische Berechnung des Beugungsintegrals I=I(v).[/size]](https://www.geogebra.org/resource/rxz6ky5v/Cj9mq5mglCQiiDOn/material-rxz6ky5v.png)
![[size=85][b]Abb.4[/b] Verteilung der Lichtintensität hinter einem Spalt entlang der Spaltenachse als Funktion des Schirmabstandes durch numerische Berechnung des Beugungsintegrals I=I(x/b).
[color=#000000]Sei {v[sub]1[/sub], v[sub]2[/sub][/color],[color=#000000]...[/color]} die Lage der Extrema des Beugungsintegrals auf der Spaltachse in Einheiten des v-Fresnel-Parameters. Mit der Formel [color=#9900ff][b]F[/b][/color][math]_i[/math]=[math]\frac{b^{^2}}{2\cdot\lambda\cdot v_i^2}[/math] können wir zu der Lage der Brennpunkte {[b][color=#ff0000]F[sub]1[/sub][/color][/b], [b][color=#0000ff]F[sub]2[/sub][/color][/b], ...} umwandeln. [b][color=#ff0000]F[sub]1[/sub][/color][/b] entspricht der Lage des [color=#ff0000][i]ersten Maximum[/i][/color] der I=I(x). Im Folgenden verwenden wir die folgende Notation: [b][color=#ff0000]Δ[sub]0λ[/sub][/color][/b]:=[b][color=#ff0000]Δ[sub]0[/sub][/color][/b]/λ -[i] Gangunterschied für den axialen und einen der äußersten Strahlen der zentralen Zone, die im ersten Brennpunkt konvergieren, pro Wellenlängeneinheit[/i] oder [b][color=#ff0000]Δ[/color][/b][sub][b][color=#ff0000]0λhalb[/color][/b][/sub]:=[b][color=#ff0000]Δ[sub]0[/sub][/color][/b]/(λ/2).
- [b]x-Koordinate der Brennpunkte[/b]:
F[math]_{i+1}[/math]=[math]\frac{\frac{b^2}{4}-\left(\Delta_0+\frac{\lambda}{2}\cdot i\right)^2}{2\cdot\left(\Delta_0+\frac{\lambda}{2}\cdot i\right)}[/math] i=0,1,... oder v-Koordinate der Brennpunkte: [math]\upsilon_{i+1}=\frac{b}{\sqrt{2\cdot\lambda\cdot F_{i+1}}}[/math].
- i[sub]max[/sub]=[b]b[/b][sub]λ[/sub]-2*[b][color=#ff0000]Δ[sub]0λ[/sub][/color][/b] -[b][i]maximale Anzahl[/i] der Brennpunkte[/b], die auf der optischen Achse sein können, kann von Bedingung →F[sub]i[/sub]≥0 gefunden werden.
- [b]y-Koordinaten der Fresnel-Zonen[/b] des Spaltes, berechnete für die Position des Punktes [b]P[/b] der Spaltenachse:
[math]\frac{b_{i+1}}{2}[/math]:=y[sub]i+1[/sub]=± [math]\sqrt{\left(\Delta_0+\frac{\lambda}{2}\cdot i\right)^2+2\cdot x\left(P\right)\cdot\left(\Delta_0+\frac{\lambda}{2}\cdot i\right)}[/math] , i=0, 1, 2, ... . [/size]](https://www.geogebra.org/resource/egvcskzz/oYJN2VtUx2t9xzrA/material-egvcskzz.png)