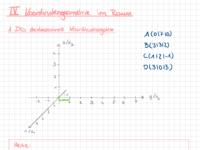
Das dreidimensionale Koordinatensystem
Um Standorte anzugeben brauchen Systeme die Hilfe der Mathematik. Dort werden Standorte als Koordinaten angegeben. Auf einem Fußballfeld kann man technisch zum Beispiel ermitteln, ob sich ein Spieler im Abseits befand oder nicht. Ganz einfach könnte man sich dies in einem zweidimensionalen Koordinatensystem veranschaulichen.
Warum?
Hefteintrag: Das dreidimensionale Koordinatensystem (abschreiben!)
Unser bisher verwendetes Koordinatensystem besteht aus zwei zueinander senkrechten Achsen. Es ermöglicht die Angabe von Punkten im zweidimensionales Raum, also in einer Ebene. Diese Punkte werden durch Zahlenpaare P(x|y) angegeben. Im Dreidimensionalen reicht uns dieses Koordinatensystem nicht mehr und wir müssen es erweitern. Verwende im folgenden Applet die Schieberegler um dir das dreidimensionale Koordinatensystem zu veranschaulichen.
Koordinaten besonderer Punkte im Koordinatensystem
Setze jeweils zwei der Koordinaten Null, z.B. P (3|0|0). Welche besondere Lage haben diese Punkte im Koordinatensystem. Formuliere einen Satz.
Setze jetzt jeweils nur eine der Koordinaten gleich Null. Welche besondere Lage haben diese Punkte im Koordinatensystem? Formuliere einen Satz.
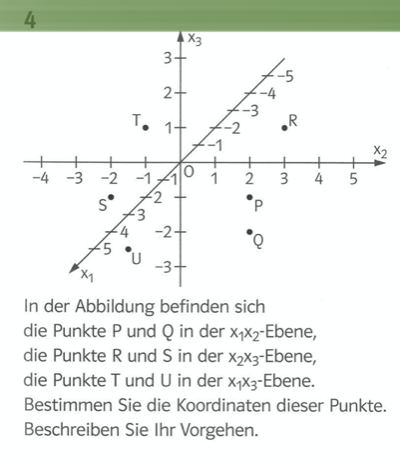
Jetzt, da wir uns schon besser im 3D-Koordinatensystem auskennen, wollen wir unser Wissen anwenden. Löse dazu die folgende Aufgabe in deinem Heft. Das Applet darunter kann dir bei der Lösung helfen. Buch S. 91
Hier kannst du die Punkte zur Veranschaulichung an den Ebenen Spiegeln. Das Werkzeug zum Spiegeln an einer Ebene findest du hier: 
. Klicke dann zuerst auf den zu spiegelnden Punkt und dann auf die Spiegelebene.
5a) Kreuze an, welche Koordinaten bei der Spiegelung an der -Ebene (xy-Ebene) gleich bleiben.
5b) Kreuze an, welche Koordinaten bei der Spiegelung an der -Ebene (yz-Ebene) gleich bleiben.
5c) Kreuze an, welche Koordinaten bei der Spiegelung an der -Ebene (xz-Ebene) gleich bleiben.
5d) Kreuze an, welche Koordinaten bei der Spiegelung am Ursprung gleich bleiben.
Zusatzfrage
Kreuze an, welche Koordinaten bei der Spiegelung an der -Achse gleich bleiben.
In einer letzten Übung solltest du auch das Zeichnen von Körpern und das Bestimmen deren Koordinaten im dreidimensionalen Koordinatensystem einüben. Löse dazu die folgende Aufgabe in deinem Heft und schicke mir ein Bild deiner Lösung im Chat bis 11:30 Uhr. Buch S. 92
Um den Stoff weiter zu vertiefen empfehle ich dir noch einige Aufgaben auf MatheGym. Außerdem findest du hier eine Anleitung, wie du dir dein eigenes kleines dreidimensionales Koordinatensystem basteln kannst. Das kann dir vor allem helfen, wenn dir das räumliche Denken noch etwas schwer fällt.
