Dreiecke
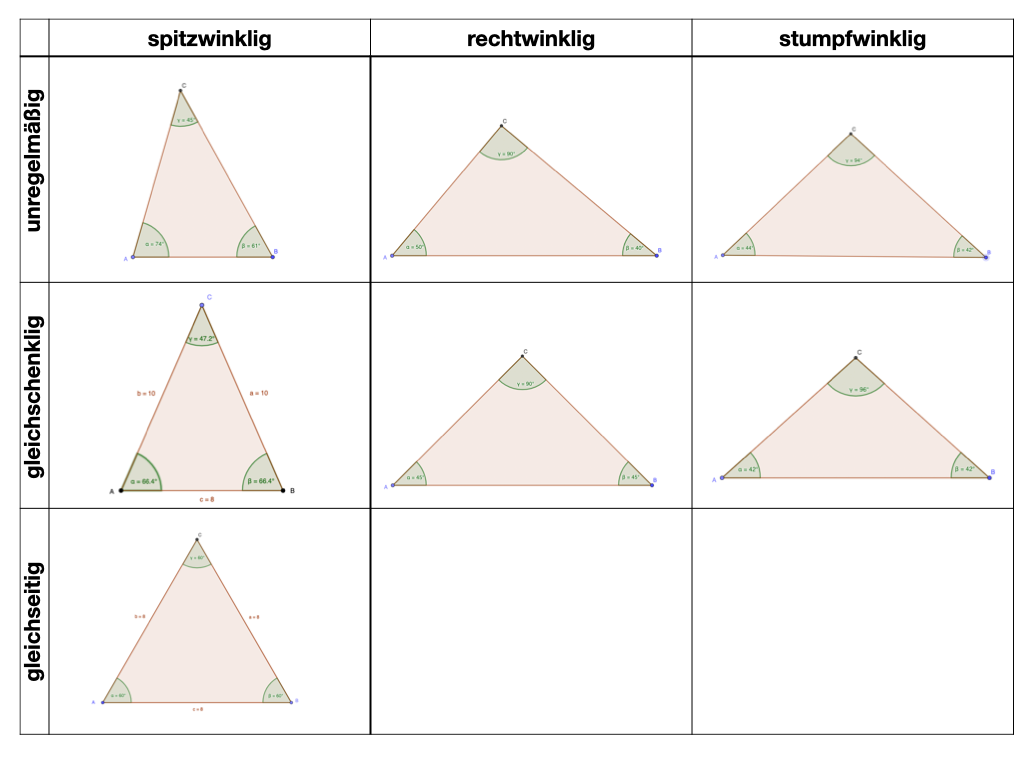
Einteilung
Nach Seitenlängen
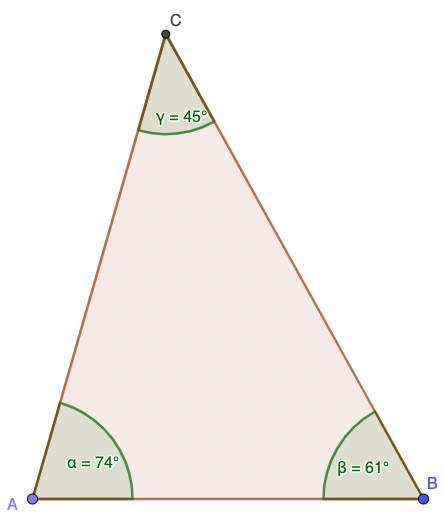
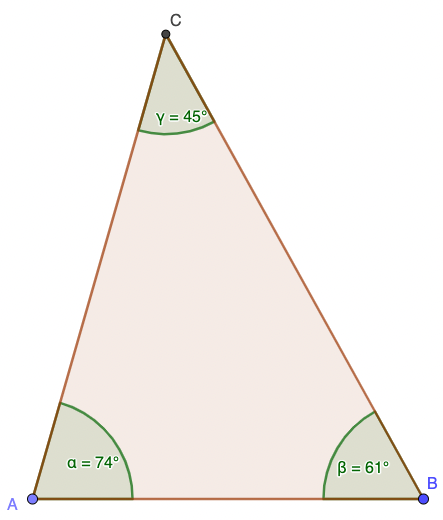
• unregelmäßige Dreiecke
• gleichschenkliges Dreieck
• Gleichseitiges Dreieck
Nach Winkeln
• Spitzwinkliges Dreieck
• Rechtwinkliges Dreieck
• Stumpfwinkliges Dreieck
Spitz- und stumpfwinklige Dreiecke werden auch unter dem Namen schiefwinkliges Dreieck zusammengefasst.
Quelle: https://de.wikipedia.org/wiki/Dreieck
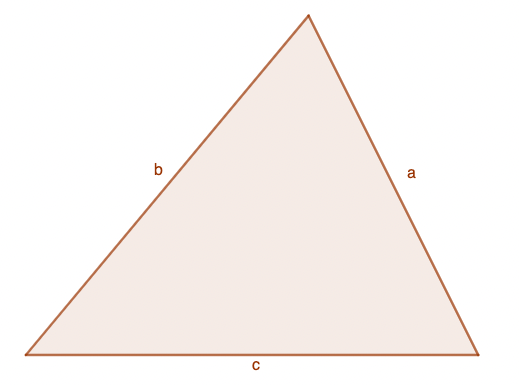
![Umfang:
u = a + b + c
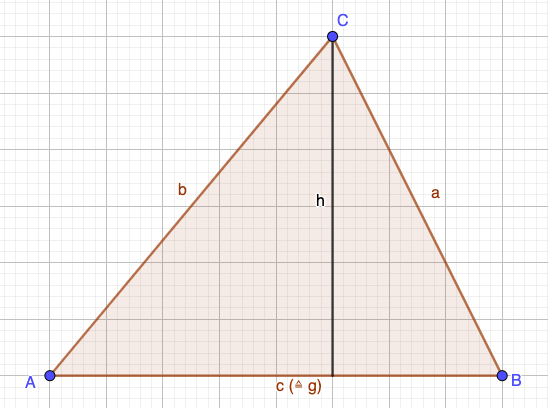
Flächeninhalt:
[math]A=\frac{1}{2}g\cdot h[/math]](https://www.geogebra.org/resource/fwyxwtca/o5AhXitcfWdY3SMw/material-fwyxwtca.png)
gleichschenkliges Dreieck
Ein gleichschenkliges Dreieck ist ein Dreieck mit mindestens zwei gleich langen Seiten. Folglich sind auch die beiden Winkel gleich groß, die den gleich langen Seiten gegenüberliegen. Zur vollständigen Bestimmung werden zwei Bestimmungsstücke benötigt, davon zumindest eine Seite.
Die beiden gleich langen Seiten heißen Schenkel, die dritte Seite heißt Basis. Der der Basis gegenüberliegende Eckpunkt heißt Spitze. Die an die Basis anliegenden Winkel heißen Basiswinkel.
Jedes gleichschenklige Dreieck ist achsensymmetrisch. Es kann spitzwinklig, rechtwinklig oder stumpfwinklig sein. Schließt die Spitze den Winkel oder ein, wird es Goldenes Dreieck erster bzw. zweiter Art genannt.
Quelle: https://de.wikipedia.org/wiki/Gleichschenkliges_Dreieck
gleichseitiges Dreieck
Ein gleichseitiges Dreieck ist ein Dreieck mit drei gleich langen Seiten bzw. Kanten sowie drei gleichen Winkeln von jeweils 60°. Ein gleichseitiges Dreieck wird auch als regelmäßiges Dreieck bezeichnet und zählt zu den regelmäßigen Polygonen. Alle gleichseitigen Dreiecke sind einander ähnlich. Gleichseitige Dreiecke sind rotationssymmetrisch (Drehung um den Mittelpunkt um 360°/3 = 120° oder Vielfache davon), spiegelsymmetrisch bezüglich der drei Mittelsenkrechten und spitzwinklig.
Quelle: https://de.wikipedia.org/wiki/Gleichseitiges_Dreieck
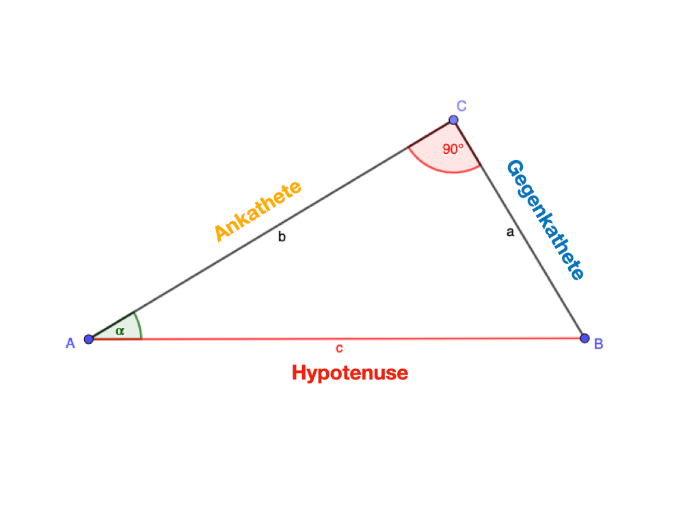
rechtwinkliges Dreieck
stumpfwinkliges Dreieck
Umfang des Dreiecks
Flächeninhalt des Dreiecks
Umfang und Flächeninhalt des Dreiecks
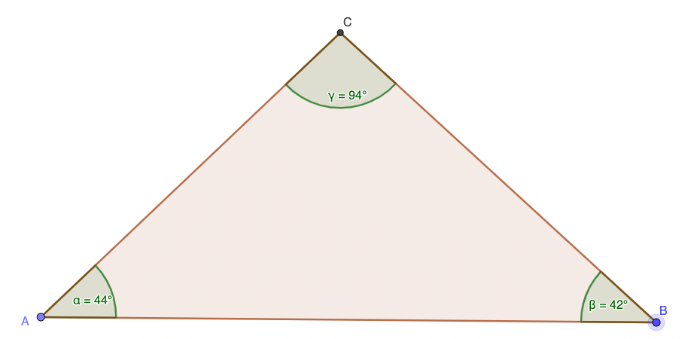
Winkelsumme im Dreieck
Die Winkelsumme im Dreieck beträgt immer 180°
Es gilt daher: α + β + γ = 180°
Mittelsenkrechte und Umkreis
Die drei Mittelsenkrechten schneiden sich in einem Punkt, dem Umkreismittelpunkt M.
M ist von allen drei Ecken gleich weit entfernt.
r ist der Umkreisradius.
Winkelhalbierende und Inkreis
Die drei Winkelhalbierenden schneiden sich in einem Punkt, dem Inkreismittelpunkt W.
Der Inkreis berührt alle drei Seiten.
r ist der Inkreisradius.
Seitenhalbierende und Schwerpunkt
Die drei Seitenhalbierenden schneiden sich in einem Punkt, dem Schwerpunkt S.
Der Schwerpunkt teilt jede Seitenhalbierende im Verhältnis 2:1.
Höhen und Höhenschnittpunkt
Die drei Höhen schneiden sich in einem Punkt, dem Höhenschnittpunkt H.
Dreieck - Höhen einblendbar
Konstruktion von Dreiecken
Dreiecke kann man mit Zirkel und Geodreieck konstruieren, obwohl man nicht alle Seiten oder Winkel kennt.
Je nachdem, ob man Seiten (S) oder Winkel (W) gegeben hat, gelten folgende Anleitungen:
SSS
Die Buchstabenfolge SSS bezeichnet die Konstruktion eines Dreieckes, bei dem alle drei Seitenlängen bekannt sind. Erstelle dir am besten zuerst eine Skizze.
Du beginnst damit, eine Seite (am besten c) zu zeichnen. Nun stellst du die Länge der Seite a an deinem Zirkel ein. Setze den Zirkel im Punkt B an (denke daran: die Seite A befindet sich gegenüber des Punktes A). Zeichne nun einen Kreisbogen.
Wiederhole das Vorangegangene mit der Seite b: Zirkel auf die Länge einstellen, in Punkt A ansetzen, Kreisbogen erzeugen. Am Schnittpunkt der Kreisbögen (Punkt C) treffen sich die Seiten. Hier kannst du sie nun mit den Punkten A und B verbinden.
Vergleiche mit der Skizze:
Hier findest du die Konstruktionsschritte:
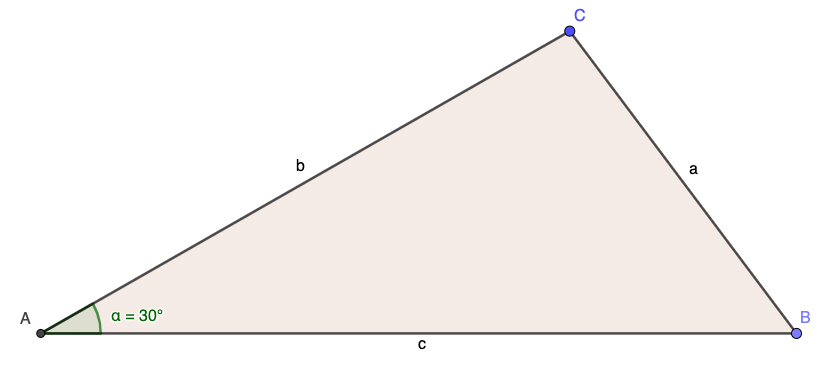
Hier findest du die Konstruktionsschritte:
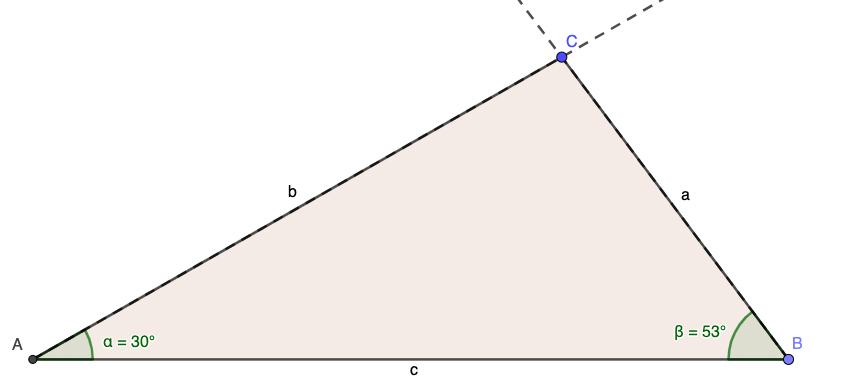
Hier findest du die Konstruktionsschritte:
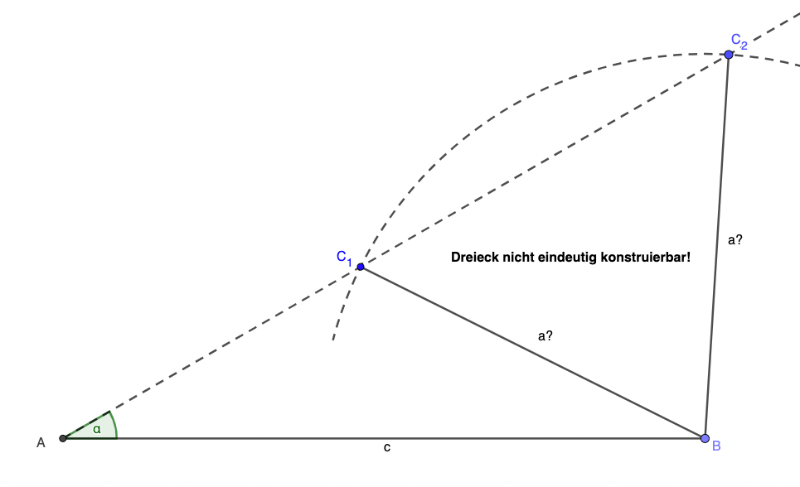
SsW
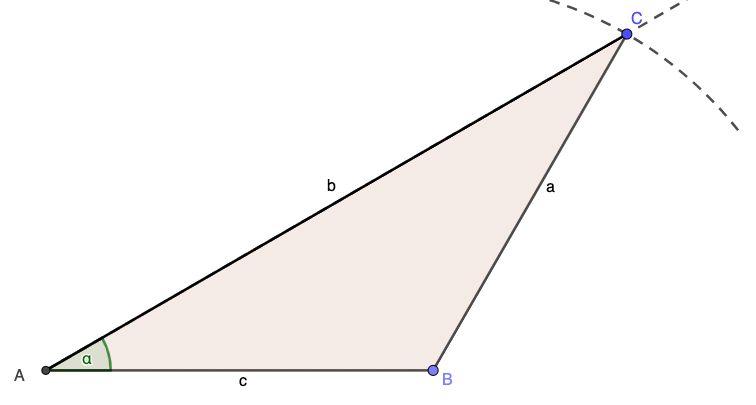
Hier findest du die Konstruktionsschritte:
Vorsicht: Sollte bei den Angaben der Winkel an der längeren Seite liegen, dann ist eine Dreieckskonstruktion nicht eindeutig möglich!