Ecriture d’une équation aux dimensions
On note [X] la dimension d’une grandeur X.
Soit G une grandeur physique. Sa dimension est notée [G]. Par exemple, si G est une longueur on écrira : [G] = L.
Pour une vitesse v, on écrira [v] = L.T-1.Écrire l’équation aux dimensions des grandeurs suivantes :
Le champ de pesanteur g (accélération)
Le poids P
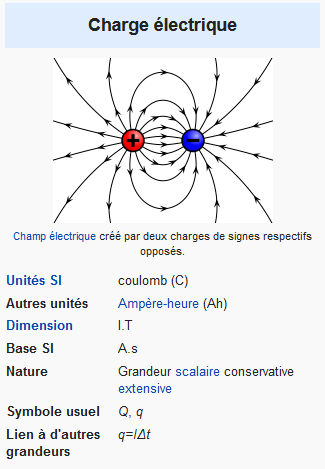
Une charge électrique Q
La masse volumique ρ
Thermomètre de Galilée

Explications
La pesanteur s'exprime en mètre par seconde au carré : m/s2. Par exemple, l'accélération normale de la pesanteur vaut 9,806 65 m/s2.
Le terme poids désigne une grandeur de la même nature qu'une force ; le poids d'un corps est le produit de la masse de ce corps par l'accélération de la pesanteur ; en particulier, le poids normal d'un corps est le produit de la masse de ce corps par l'accélération normale de la pesanteur ;
Dans le système international d'unités, la charge électrique à pour unités le coulomb, de symbole C, qui constitue une unité dérivée, dont le nom vient de celui du physicien français Charles-Augustin Coulomb. Par définition, c'est la quantité de charge transportée en 1 seconde par un courant électrique ayant une intensité de 1 ampère2. Par suite 1 C = 1 A.s, et la charge électrique Q a pour dimensions [Q]=A.T.
L'unité de mesure de la masse volumique dans le Système international est le kilogramme par mètre cube (kg m−3). Dans le système CGS, elle s'exprime en g cm−3, ce qui a l'avantage de donner des valeurs numériques de l'ordre de l'unité pour les solides dans les conditions normales de température et de pression (CNTP).
On utilise couramment le g cm−3, le kg L−1 ou la t m−3 (ces trois dernières unités étant numériquement équivalentes) ou toute autre unité exprimée par le rapport d'une unité de masse et d'une unité de volume.